深入理解向量场微积分

向量场的基本概念

向量场（Vector Field）是描述空间中每一点具有特定方向和大小的向量的函数。向量场广泛应用于描述自然界中的各种现象，如电场、磁场、重力场以及流体的速度场等。本节将详细介绍向量场的定义、与标量场的区别以及典型的向量场实例。

向量场的定义

向量场（Vector Field）是一个赋予空间中每一点一个向量的函数。更形式化地，设 $M$ 是一个 $n$ -维光滑流形（在此讨论的主要是三维欧几里得空间 $\mathbb{R}^3$ ），则一个向量场 $\mathbf{F}$ 在 $M$ 上是一个光滑的赋值函数：


$$
\mathbf{F} : M \rightarrow \mathbb{R}^3
$$

对于 $M$ 中的每一点 $\mathbf{p}$ ， $\mathbf{F}(\mathbf{p})$ 是一个三维向量，表示在该点的向量值。例如，在欧几里得空间中，向量场可以表示为：


$$
\mathbf{F}(x, y, z) = \langle F_x(x, y, z), F_y(x, y, z), F_z(x, y, z) \rangle
$$

其中， $F_x, F_y, F_z$ 是定义在空间中的标量函数，分别表示向量在 $x, y, z$ 方向的分量。

3-维光滑流形：可以简单理解为：流形意味着局部看起来像普通的（这里三维）欧几里得空间。光滑意味着它的结构足够平滑，没有尖锐的拐角或断点。数学上，这意味着流形上的函数是可微的，并且可以有连续的导数。

标量场与向量场的区别

标量场（Scalar Field）和向量场都是场的一种类型，用于描述空间中随位置变化的物理量。它们的主要区别在于：

值的类型：
- 标量场在每一点上的取值是一个标量（通常指一个实数）。
- 向量场在每一点上的取值是一个向量，具有大小和方向。
数学表达：
- 标量场通常表示为 $\phi : M \rightarrow \mathbb{R}$ 。
- 向量场表示为 $\mathbf{F} : M \rightarrow \mathbb{R}^N$ 。

示例比较：

温度分布：在空间中每一点的温度可以用一个标量表示，是一个标量场。
电场：在空间中每一点的电场强度具有大小和方向，用向量表示，是一个向量场。

向量场的例子

向量场在物理学中具有广泛的应用，以下是几个典型的向量场实例：

1. 重力场（Gravitational Field）

重力场描述了空间中每一点的引力作用，是一个向量场。对于_地球表面_的重力场，可以近似认为每一点的重力向量指向地球的中心，大小与重力加速度 $\mathbf{g}$ 有关，通常表示为：


$$
\mathbf{g} = \langle 0, 0, -g \rangle
$$

其中， $g \approx 9.81 \, \text{m/s}^2$ 是重力加速度的大小。

多个天体形成的重力场（等势面描述）

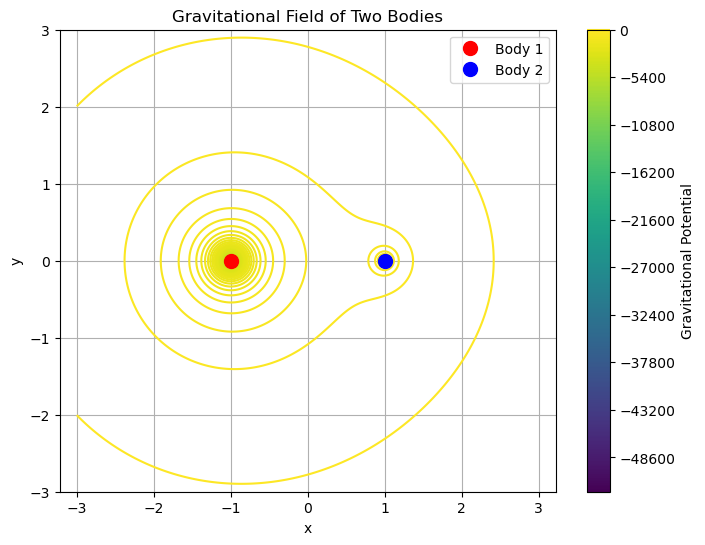
2. 电场（Electric Field）

电场是描述电荷之间作用力的向量场。由带电粒子产生的电场 $\mathbf{E}$ 可以在空间中的每一点表示为一个向量，方向表示受力方向，大小与该点的电场强度相关。对于点电荷 $Q$ 而言，其产生的电场在空间中每一点的表达式为：


$$
\mathbf{E}(\mathbf{r}) = \frac{1}{4\pi \varepsilon_0} \cdot \frac{Q}{|\mathbf{r}|^3} \mathbf{r}
$$

其中， $\mathbf{r}$ 是从电荷位置指向空间中任一点的矢量， $\varepsilon_0$ 是真空的电容率。

3. 速度场（Velocity Field）

速度场用于描述流体或气体在空间中不同位置的流动速度，是一个向量场。对于一个流体在空间中的运动，速度场可以表示为：


$$
\mathbf{v}(x, y, z) = \langle v_x(x, y, z), v_y(x, y, z), v_z(x, y, z) \rangle
$$

其中， $v_x, v_y, v_z$ 分别表示流体在 $x, y, z$ 方向的速度分量。速度场在流体力学中起着关键作用，用于分析和预测流体的行为。

4. 磁场（Magnetic Field）

磁场是描述磁力作用的向量场。由电流或磁性材料产生的磁场 $\mathbf{B}$ 在空间中的每一点都有一个方向和大小。对于无限长直导线产生的磁场，其表达式为：


$$
\mathbf{B}(\mathbf{r}) = \frac{\mu_0 I}{2\pi r} \hat{\phi}
$$

其中， $\mu_0$ 是真空的磁导率， $I$ 是电流强度， $r$ 是距离导线的径向距离， $\hat{\phi}$ 是围绕导线的单位环向量。

向量场的可视化

由于向量场在空间中每一点都关联一个向量，因此可视化向量场需要借助箭头或流线等方法。箭头图法通过在空间中的不同位置绘制箭头，方向和长度分别表示向量的方向和大小。流线法则通过绘制流体或场的流线，展示向量场的整体流动趋势。

import numpy as np
import matplotlib.pyplot as plt

# Generate grid
x, y = np.meshgrid(np.linspace(-2, 2, 20), np.linspace(-2, 2, 20))

u = x**2 - y
v = y**2 + x


plt.figure(figsize=(6, 6))
plt.quiver(x, y, u, v, color='r', pivot='mid')
plt.title('Quiver Plot Example')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.grid()
plt.axis('equal')
plt.show()

import numpy as np
import matplotlib.pyplot as plt

# Generate grid
x, y = np.meshgrid(np.linspace(-2, 2, 100), np.linspace(-2, 2, 100))

u = x**2 - y
v = y**2 + x

plt.figure(figsize=(6, 6))
plt.streamplot(x, y, u, v, color='b', density=1.5, linewidth=1, arrowsize=1)
plt.title('Streamplot Example')
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
plt.grid()
plt.axis('equal')
plt.show()

gh|500

向量场的性质

向量场具有多种性质和运算，例如：

保守场（Conservative Field）：向量场如果可以表示为某个标量势函数的梯度，则称为保守场。即存在标量函数 $\phi$ 使得：


$$
   \mathbf{F} = \nabla \phi
$$

保守场的一个重要性质是其环路积分为零。

散度（Divergence）：散度是标量运算符，用于度量向量场在某一点的发散程度。数学表达式为：


$$
   \nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}
$$

旋度（Curl）：旋度是向量运算符，用于度量向量场在某一点的旋转程度。数学表达式为：


$$
   \nabla \times \mathbf{F} = \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}, \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}, \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right)
$$

我们会在_后文_详细说明这些性质。

基本运算

向量运算包括向量的加法、减法、数乘、点积（内积）和叉积（外积）等基本操作。这些运算构成了向量空间的基础，为后续的微分运算奠定了数学基础。

向量加法和减法

两个向量的加法定义为对应分量的逐一相加，几何上表现为首尾相接的方法。例如，若有向量 $\mathbf{a} = (a_1, a_2, a_3)$ 和 $\mathbf{b} = (b_1, b_2, b_3)$ ，则它们的和为：


$$
\mathbf{a} + \mathbf{b} = (a_1 + b_1,\, a_2 + b_2,\, a_3 + b_3)
$$

向量的减法则类似，


$$
\mathbf{a} - \mathbf{b} = (a_1 - b_1,\, a_2 - b_2,\, a_3 - b_3)
$$

数乘

向量与标量（实数）的乘法称为数乘。对于向量 $\mathbf{a} = (a_1, a_2, a_3)$ 和标量 $k$ ，数乘运算定义为：


$$
k\mathbf{a} = (k a_1,\, k a_2,\, k a_3)
$$

数乘改变了向量的长度（模），但不改变其方向，除非标量为负数，此时向量方向相反。

点积（内积）

点积是向量运算中的重要概念，定义为两个向量对应分量的乘积之和。对于向量 $\mathbf{a}$ 和 $\mathbf{b}$ ，点积定义为：


$$
\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3
$$

点积具有多种几何意义，例如，它等于两个向量模的乘积与它们夹角余弦的乘积：


$$
\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos\theta
$$

其中 $\theta$ 为向量 $\mathbf{a}$ 和 $\mathbf{b}$ 之间的夹角。点积在投影、功的计算以及测量向量之间的相互关系等方面具有重要应用。

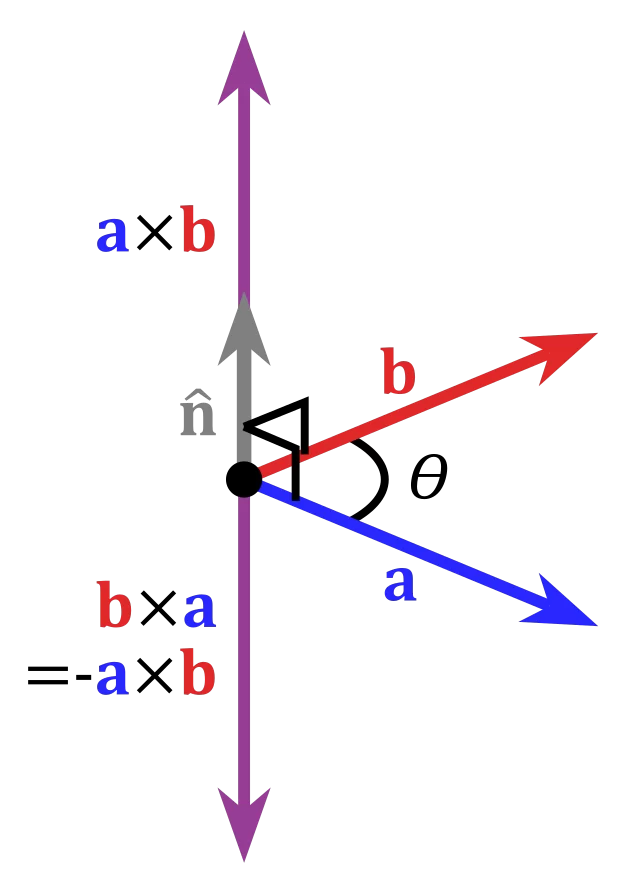
右手定则

右手定则用于确定叉积向量的方向。具体方法是：

伸开右手，使拇指、食指和中指互相垂直。
让拇指指向 $\mathbf{a}$ 的方向，食指指向 $\mathbf{b}$ 的方向。
此时，中指所指的方向就是 $\mathbf{a} \times \mathbf{b}$ 的方向。

当然，你不用真的去比划，而是记住空间相对关系就行，结合下面的图。

gh|200

叉积

叉积（也称为向量积）是两个向量在三维空间中的一种运算，结果是一个新的向量。叉积的结果向量垂直于原来的两个向量，并且其方向由右手定则确定。叉积的大小等于原来两个向量所构成的平行四边形的面积。

假设我们有两个向量 $\mathbf{a}$ 和 $\mathbf{b}$ ，它们的分量分别为：


$$
\mathbf{a} = \langle a_1, a_2, a_3 \rangle
$$


$$
\mathbf{b} = \langle b_1, b_2, b_3 \rangle
$$

那么， $\mathbf{a}$ 和 $\mathbf{b}$ 的叉积 $\mathbf{a} \times \mathbf{b}$ 定义为：


$$
\mathbf{a} \times \mathbf{b} = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3
\end{vmatrix}
$$

这个行列式展开后，可以得到：


$$
\mathbf{a} \times \mathbf{b} = \left( a_2 b_3 - a_3 b_2 \right) \mathbf{i} - \left( a_1 b_3 - a_3 b_1 \right) \mathbf{j} + \left( a_1 b_2 - a_2 b_1 \right) \mathbf{k}
$$

或者写成向量形式：


$$
\mathbf{a} \times \mathbf{b} = \langle a_2 b_3 - a_3 b_2, a_3 b_1 - a_1 b_3, a_1 b_2 - a_2 b_1 \rangle
$$

叉积的性质

反交换性：


$$
\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a})
$$

分配律：


$$
\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}
$$

与标量的关系：


$$
(c \mathbf{a}) \times \mathbf{b} = c (\mathbf{a} \times \mathbf{b})
$$


$$
\mathbf{a} \times (c \mathbf{b}) = c (\mathbf{a} \times \mathbf{b})
$$

其中 $c$ 是标量。

向量模的关系：叉积的模等于两个向量模的乘积与它们夹角的正弦值：


$$
\|\mathbf{a} \times \mathbf{b}\| = \|\mathbf{a}\| \|\mathbf{b}\| \sin \theta
$$

其中 $\theta$ 是 $\mathbf{a}$ 和 $\mathbf{b}$ 之间的夹角。

微分运算

梯度（Gradient）

梯度是一个向量微分算子，用于描述标量场中函数的最大变化率方向。对于一个标量函数 $f(x, y, z)$ ，其梯度定义为：


$$
\nabla f = \left( \frac{\partial f}{\partial x},\, \frac{\partial f}{\partial y},\, \frac{\partial f}{\partial z} \right)
$$

几何上，梯度向量在某点的方向指向函数 $f$ 增加最快的方向，其大小等于在该方向上的最大增加率。

梯度作用于一个标量场，结果是一个向量场。

例子

在物理学中，梯度的一个典型应用是描述温度场。例如，若 $T(x, y, z)$ 表示空间中某一位置的温度分布，则梯度 $\nabla T$ 表示温度变化最快的方向和速率。在热传导过程中，热流量通常与温度梯度成正比，这一关系由傅里叶定律（Fourier’s Law）描述：


$$
\mathbf{q} = -k \nabla T
$$

其中， $\mathbf{q}$ 是热流密度， $k$ 是热导率。

散度（Divergence）

散sàn度是向量场的一个标量微分算子，用于度量向量场在某点的源或汇程度。对于向量场 $\mathbf{F} = (F_x, F_y, F_z)$ ，散度定义为微分算子与向量场的点积：


$$
\nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}
$$

散度作用于一个向量场，结果是一个标量场。

考虑一个非常小的体积元素（例如一个微小的立方体）：

散度为正：如果该体积元素的体积在增大，说明有更多的流体从这个小立方体流出，而不是流入，称为源。
散度为负：如果该体积元素的体积在减小，说明有更多的流体流入这个小立方体，而不是流出，称为汇。
为零表示既不流入也不流出。

通过小体积分析散度

为了将代数定义与几何含义联系起来，我们可以考虑一个位于点 $\mathbf{P} = (x, y, z)$ 附近的一个小立方体（称为微小体积），其边长趋近于零。

流出量的计算：
- 想象 $F$ 是有向的水流，则可以分解为三个维度的分量 $F_x, F_y, F_z$
- 沿 $x$ 轴正方向的面上的流出量约为 $F_x \cdot A = F_x \cdot (\Delta y \Delta z)$ 。
- 沿 $x$ 轴负方向的面上的流入量约为 $F_x(x - \Delta x, y, z) \cdot A = \left(F_x - \frac{\partial F_x}{\partial x} \Delta x\right) \Delta y \Delta z$ 。
  - 这里用到了泰勒展开 $f(x - \Delta x) \approx f(x) - f'(x) \Delta x$
  - $F_x(x - \Delta x, y, z)$ 相当于前一个小体积的流出量，代表了当前小体积的流入量。
净流出量沿 $x$ 轴方向约为：


$$
   \left(F_x - \left(F_x - \frac{\partial F_x}{\partial x} \Delta x\right)\right) \Delta y \Delta z = \frac{\partial F_x}{\partial x} \Delta x \Delta y \Delta z
$$

类似的，净流出量沿 $y$ 和 $z$ 轴方向分别为 $\frac{\partial F_y}{\partial y} \Delta x \Delta y \Delta z$ 和 $\frac{\partial F_z}{\partial z} \Delta x \Delta y \Delta z$ 。

总净流出量：

将三个方向的净流出量相加：


$$
   \left(\frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z}\right) \Delta x \Delta y \Delta z = (\nabla \cdot \mathbf{F}) \Delta V
$$

其中， $\Delta V = \Delta x \Delta y \Delta z$ 是微小体积。

散度的定义：散度定义为单位体积内的净流出量，因此：


$$
   \nabla \cdot \mathbf{F} = \lim_{\Delta V \to 0} \frac{\text{净流出量}}{\Delta V}
$$

正是这样，代数上的散度 $\nabla \cdot \mathbf{F}$ 量化了点 $\mathbf{P}$ 处单位体积内的净流出量。

散度在物理中的应用

在流体力学中，散度用于描述流体的连续性方程。假设流体的速度场为 $\mathbf{v}$ ，则流体的质量守恒可以表示为：


$$
\nabla \cdot \mathbf{v} + \frac{\partial \rho}{\partial t} = 0
$$

其中， $\rho$ 是流体密度。

这个方程表明：流体的密度变化与流体的流入流出有关。流入多于流出，密度增加；反之，密度减少。

如果流体是不可压缩的（即 $\rho$ 恒定），则散度为零：


$$
\nabla \cdot \mathbf{v} = 0
$$

这表示流体在任意点的流入量等于流出量，流体体积保持不变。

旋度（Curl）

旋度的定义和几何意义

旋度是向量场的一个向量微分算子，用于度量向量场中局部的旋转性质。对于向量场 $\mathbf{F} = (F_x, F_y, F_z)$ ，旋度定义为：


$$
\nabla \times \mathbf{F} = \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z},\, \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x},\, \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right)
$$

几何上，旋度的方向沿旋转轴，大小代表旋转的强度，正负表示旋转的逆顺。如果旋度不为零，表示向量场在该点附近存在旋转或涡流。

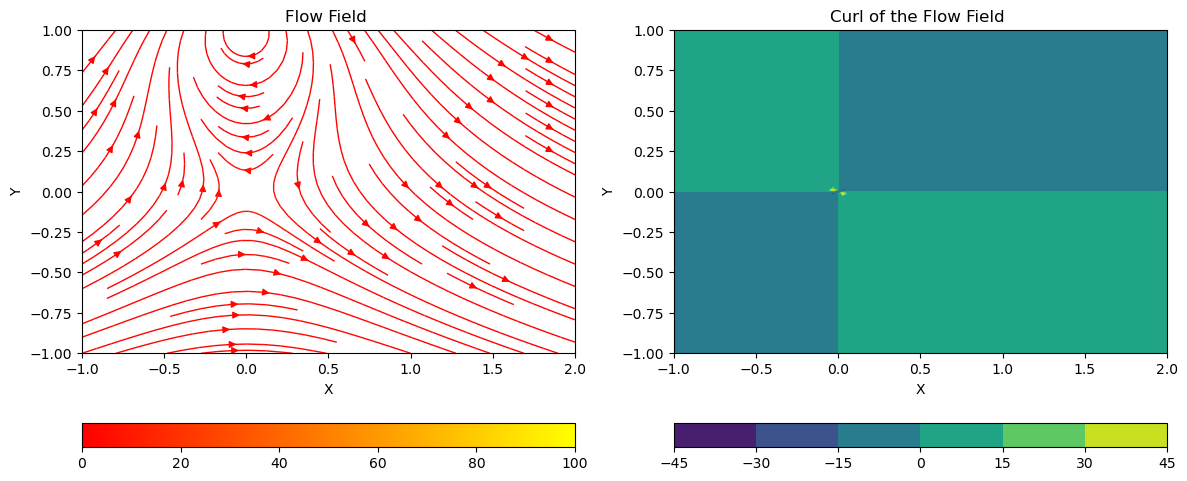
对于一个二维速度场 $\mathbf{v} = (u, v)$ ，旋度是标量，定义为：


$$
\text{curl} = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}
$$

可以用颜色梯度来表示旋度的大小和方向。正代表逆旋，负代表顺旋。

如果是三维流场，旋度场会有三个分量，表示为向量场：


$$
\mathbf{\omega} = \nabla \times \mathbf{v}
$$

旋度向量的每个分量代表流体旋转的不同方向的强度。

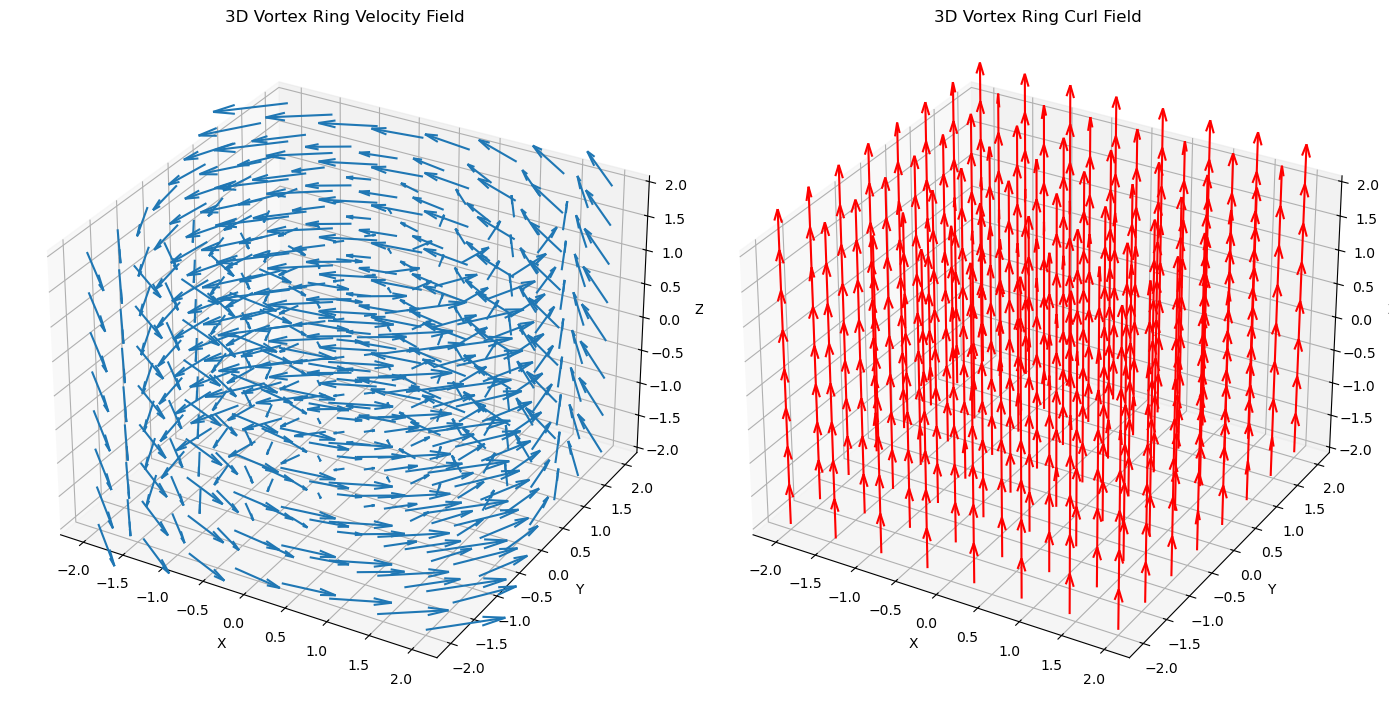
在上图中（注：长度已经归一化，不再具备意义），旋度场每个向量都指向 $+z$ ，这意味着：

场的旋转轴平行于 $z$ 轴。
旋转方向是逆时针（从正 $z$ 轴看去）。
旋转的强度由旋度向量的大小决定。

把左边的场看作电场，则右侧结果和右手螺旋定则一致。

 1import numpy as np
 2import matplotlib.pyplot as plt
 3
 4# 定义网格
 5x = np.linspace(-2, 2, 8)
 6y = np.linspace(-2, 2, 8)
 7z = np.linspace(-2, 2, 8)
 8X, Y, Z = np.meshgrid(x, y, z)
 9
10# 定义涡流环速度场
11U = -Y
12V = X
13W = np.zeros_like(X)
14
15# 计算旋度场
16dW_dy, dW_dx, dW_dz = np.gradient(W, y, x, z, edge_order=2)
17dV_dy, dV_dx, dV_dz = np.gradient(V, y, x, z, edge_order=2)
18dU_dy, dU_dx, dU_dz = np.gradient(U, y, x, z, edge_order=2)
19
20curl_x = dW_dy - dV_dz
21curl_y = dU_dz - dW_dx
22curl_z = dV_dx - dU_dy
23
24# 可视化速度场
25fig = plt.figure(figsize=(14, 7))
26
27ax1 = fig.add_subplot(121, projection='3d')
28ax1.quiver(X, Y, Z, U, V, W, length=0.3, normalize=False)
29ax1.set_title('3D Vortex Ring Velocity Field')
30ax1.set_xlabel('X')
31ax1.set_ylabel('Y')
32ax1.set_zlabel('Z')
33
34# 可视化旋度场
35ax2 = fig.add_subplot(122, projection='3d')
36ax2.quiver(X, Y, Z, curl_x, curl_y, curl_z, length=0.3, color='r', normalize=False)
37ax2.set_title('3D Vortex Ring Curl Field')
38ax2.set_xlabel('X')
39ax2.set_ylabel('Y')
40ax2.set_zlabel('Z')
41
42plt.tight_layout()
43plt.show()

旋度在电磁场中的应用

在电磁学中，旋度在描述电场和磁场的动态关系中起着关键作用。特别是麦克斯韦方程组中的旋度方程：

法拉第电磁感应定律：


$$
\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t}
$$

安培-麦克斯韦定律：


$$
\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \epsilon_0 \frac{\partial \mathbf{E}}{\partial t}
$$

这些方程表明，时间变化的磁场会产生一个旋转的电场，反之亦然，揭示了电磁场中的旋转性质。

拉普拉斯算子（Laplacian）

拉普拉斯算子的定义和性质

拉普拉斯算子是一个标量微分算子，定义为散度的梯度。对于标量函数 $f(x, y, z)$ ，拉普拉斯算子记作 $\nabla^2 f$ 或 $\Delta f$ ，其定义为：


$$
\nabla^2 f = \nabla \cdot (\nabla f) = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}
$$

拉普拉斯算子具有以下性质：

线性性： $\nabla^2 (af + bg) = a \nabla^2 f + b \nabla^2 g$ ，其中 $a, b$ 为常数。
交换性：混合二阶偏导数的交换律，即 $\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$ 。

几何性质：

拉普拉斯算子在旋转下是不变的，因为它对称考虑了相关点邻域中的所有点。
拉普拉斯算子可以看作对标量的二阶导平均值，它反应了该点偏离平均的程度。

从几何角度

拉普拉斯方程和物理应用

拉普拉斯方程是形如 $\nabla^2 f = 0$ 的偏微分方程。其解称为调和函数（Harmonic Function），具有许多重要的数学性质，如最大值原理。

gh|400

泊松方程则是拉普拉斯方程的推广，形如 $\nabla^2 f = \rho$ ，其中 $\rho$ 是已知函数。泊松方程在电磁学和引力场中描述潜在场的分布。

gh|400

在物理学中，拉普拉斯方程和泊松方程广泛应用于：

静电场：在无电荷区域，电势函数 $\phi$ 满足拉普拉斯方程 $\nabla^2 \phi = 0$ ；在有电荷分布时，满足泊松方程 $\nabla^2 \phi = -\frac{\rho}{\epsilon_0}$ 。
引力场：在质量分布 $\rho$ 的影响下，引力势 $\Phi$ 满足泊松方程 $\nabla^2 \Phi = 4 \pi G \rho$ ，其中 $G$ 是引力常数。
稳态热传导：在稳态条件下，温度分布 $T$ 满足拉普拉斯方程 $\nabla^2 T = 0$ 。

拉普拉斯算子边缘检测

平均二阶导越接近 0，意味着此处的变化越剧烈。

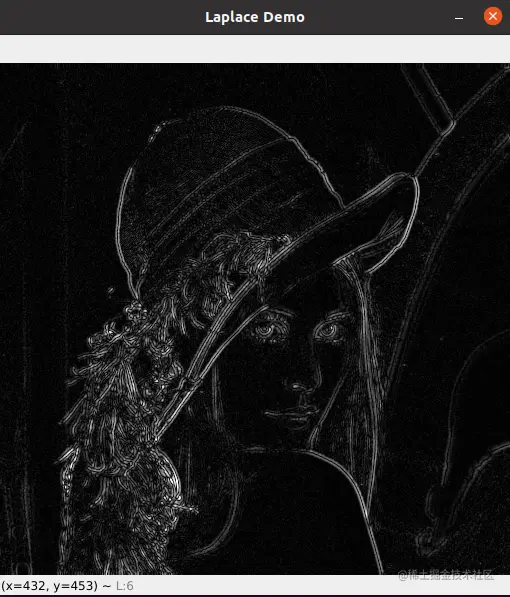
引自：https://docs.opencv.org/3.4/d5/db5/tutorial_laplace_operator.html

在之前的教程中，我们学习了如何使用 Sobel 运算符。它基于这样的事实：在边缘区域，像素强度表现出“跳跃”或强度的高变化。获得强度的一阶导数，我们观察到边缘具有最大值，如图所示：
而且……如果我们采用二阶导数会发生什么？

您可以观察到二阶导数为零！因此，我们也可以使用这个标准来尝试检测图像中的边缘。但请注意，零不仅会出现在边缘中（它们实际上也可能出现在其他无意义的位置）；这可以通过在需要时应用过滤来解决。

输入：

gh|250

输出：

gh|250

矩阵算子

雅可比矩阵（Jacobian Matrix）

梯度是标量函数的偏导数向量，而雅可比矩阵是向量值函数的偏导数矩阵。可以认为梯度是雅可比矩阵的一个特例，即当 m=1 时，雅可比矩阵退化为梯度向量。

定义

雅可比矩阵（Jacobian Matrix）是描述向量值函数的一阶偏导数的矩阵。对于一个从 $\mathbb{R}^n$ 到 $\mathbb{R}^m$ 的向量函数 $\mathbf{F}: \mathbb{R}^n \to \mathbb{R}^m$ ，其雅可比矩阵定义为：


$$
J(\mathbf{F}) =
\begin{bmatrix}
\frac{\partial F_1}{\partial x_1} & \frac{\partial F_1}{\partial x_2} & \cdots & \frac{\partial F_1}{\partial x_n} \\
\frac{\partial F_2}{\partial x_1} & \frac{\partial F_2}{\partial x_2} & \cdots & \frac{\partial F_2}{\partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial F_m}{\partial x_1} & \frac{\partial F_m}{\partial x_2} & \cdots & \frac{\partial F_m}{\partial x_n}
\end{bmatrix}
$$

性质

线性近似：雅可比矩阵提供了向量函数在某点的线性近似，即通过泰勒展开的一阶部分。
可逆性：当雅可比矩阵在某点为方阵且行列式非零时，依据逆函数定理，该点附近存在该函数的局部逆映射。
变换性质：雅可比矩阵在坐标变换和非线性变换中起关键作用，尤其在多变量积分的变量替换中。

雅可比行列式（Jacobian Determinant）

雅可比行列式是雅可比矩阵的行列式，记为 $\det(J(\mathbf{F}))$ 。它在坐标变换和多变量积分中用于衡量微分体积的伸缩因子。例如，在进行变量替换积分时，积分区域的体积元素通过雅可比行列式来调整。

黑塞矩阵（Hessian Matrix）

定义

黑塞矩阵（Hessian Matrix）是一个由二阶偏导数组成的方阵，用于描述多变量函数的二阶导数信息。对于一个具有二阶连续偏导数的标量函数 $f: \mathbb{R}^n \to \mathbb{R}$ ，其黑塞矩阵定义为：


$$
H(f) = 
\begin{bmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}
\end{bmatrix}
$$

性质

对称性：在函数 $f$ 的二阶偏导数连续的情况下，依据克莱罗定理（Clairaut’s Theorem），黑塞矩阵是对称的，即 $\frac{\partial^2 f}{\partial x_i \partial x_j} = \frac{\partial^2 f}{\partial x_j \partial x_i}$ 。
二阶近似：在泰勒展开中，黑塞矩阵提供了二阶近似，用于描述函数在某一点附近的曲率性质。
正定性与极值：黑塞矩阵的正定性、负定性或不定性决定了函数在某临界点的极值类型（局部最小、局部最大或鞍点）。

在物理学和工程学中，曲线（Curve）和曲面（Surface）是描述空间中物体形状和运动的重要工具。本章将系统地介绍参数曲线和参数曲面的定义与表示，切向量（Tangent Vector）与法向量（Normal Vector）的计算方法，以及弧长（Arc Length）、曲率（Curvature）、挠率（Torsion）的定义与计算，并深入探讨Frenet-Serret公式。这些内容不仅在几何学中具有重要意义，也在物理学中的运动学、力学等领域有广泛应用。

参数曲线和参数曲面

参数化曲线的定义与表示

参数曲线是通过一个或多个参数来描述空间中点的位置随参数变化而变化的路径。在数学上，一个参数曲线可以表示为一个向量值函数：


$$
\mathbf{r}(t) = \begin{pmatrix}
x(t) \\
y(t) \\
z(t)
\end{pmatrix}, \quad t \in I
$$

其中， $\mathbf{r}(t)$ 是曲线在参数 $t$ 时刻的位置向量， $I$ 是参数的定义域。参数曲线通常用于描述物体的运动轨迹、流体的路径线等。

示例： 圆的参数方程

在三维空间中，xOy 平面的单位圆可以参数化为：


$$
\mathbf{r}(t) = \begin{pmatrix}
\cos t \\
\sin t \\
0
\end{pmatrix}, \quad t \in [0, 2\pi)
$$

参数化曲面的定义与表示

参数曲面是通过两个或多个参数来描述空间中点的位置随参数变化而变化的表面。一般情况下，参数曲面可以表示为向量值函数：


$$
\mathbf{r}(u, v) = \begin{pmatrix}
x(u, v) \\
y(u, v) \\
z(u, v)
\end{pmatrix}, \quad (u, v) \in D
$$

其中， $\mathbf{r}(u, v)$ 是曲面上点的位置向量， $D$ 是参数的定义域。参数曲面常用于描述物体的表面形状，如球面、抛物面等。

示例： 球面的参数方程

半径为 $R$ 的球面可以参数化为：


$$
\mathbf{r}(\theta, \phi) = \begin{pmatrix}
R \sin \theta \cos \phi \\
R \sin \theta \sin \phi \\
R \cos \theta
\end{pmatrix}, \quad \theta \in [0, \pi], \quad \phi \in [0, 2\pi)
$$

切向量与法向量的计算

切向量

参数曲线的切向量

对于参数曲线 $\mathbf{r}(t)$ ，切向量 $\mathbf{T}(t)$ 定义为参数 $t$ 的导数：


$$
\mathbf{T}(t) = \frac{d\mathbf{r}(t)}{dt} = \begin{pmatrix}
x'(t) \\
y'(t) \\
z'(t)
\end{pmatrix}
$$

切向量表示曲线在点 $\mathbf{r}(t)$ 处的切方向，其方向与曲线的运动方向一致。

参数曲面的切向量

对于参数曲面 $\mathbf{r}(u, v)$ ，在点 $(u, v)$ 处存在两个基本的切向量，分别沿参数 $u$ 和 $v$ 的方向：


$$
\mathbf{r}_u = \frac{\partial \mathbf{r}}{\partial u} = \begin{pmatrix}
\frac{\partial x}{\partial u} \\
\frac{\partial y}{\partial u} \\
\frac{\partial z}{\partial u}
\end{pmatrix}, \quad
\mathbf{r}_v = \frac{\partial \mathbf{r}}{\partial v} = \begin{pmatrix}
\frac{\partial x}{\partial v} \\
\frac{\partial y}{\partial v} \\
\frac{\partial z}{\partial v}
\end{pmatrix}
$$

这两个切向量构成了曲面在该点的切平面。

法向量

参数曲线的法向量

对于参数曲线 $\mathbf{r}(t)$ ，法向量 $\mathbf{N}(t)$ 通常定义为标准化切向量，即切向量的单位法向量，用以描述曲线的局部几何性质：


$$
\mathbf{N}(t) = \frac{\mathbf{T}'(t)}{|\mathbf{T}'(t)|}
$$

参数曲面的法向量

对于参数曲面 $\mathbf{r}(u, v)$ ，法向量 $\mathbf{N}(u, v)$ 可以通过两个基本切向量的叉乘得到：


$$
\mathbf{N}(u, v) = \frac{\mathbf{r}_u \times \mathbf{r}_v}{|\mathbf{r}_u \times \mathbf{r}_v|}
$$

法向量垂直于切平面，指示曲面的局部方向。

弧长和曲率

弧长公式的推导与应用

对于参数曲线 $\mathbf{r}(t)$ ，从参数 $t_0$ 到 $t$ 的弧长 $s(t)$ 定义为：


$$
s(t) = \int_{t_0}^{t} |\mathbf{r}'(\tau)| d\tau = \int_{t_0}^{t} \sqrt{x'(\tau)^2 + y'(\tau)^2 + z'(\tau)^2} d\tau
$$

推导过程：

微分弧长： 在参数 $t$ 处，微小的弧长增量 $ds$ 与参数增量 $dt$ 之间的关系为：


$$
   ds = |\mathbf{r}'(t)| dt
$$

积分累加： 将微分式两边积分，得到从 $t_0$ 到 $t$ 的总弧长：


$$
   s(t) = \int_{t_0}^{t} |\mathbf{r}'(\tau)| d\tau
$$

弧长参数化（Arc-length Parameterization）是将参数 $t$ 换为弧长 $s$ 的过程，即 $s = s(t)$ 。这种参数化在分析曲线的几何性质时尤为重要，因为它消除了参数速度的影响，使得切向量的长度始终为单位长度。

曲率向量和曲率是描述曲线和曲面几何性质的重要概念。下面我将分别介绍它们。

曲率向量

曲率向量（Curvature Vector）是描述曲线在某一点的弯曲程度和方向的向量。对于空间曲线，曲率向量定义为曲线的加速度向量在法向方向上的分量。具体来说，设有参数曲线 $\mathbf{r}(t)$ ，它的曲率向量 $\mathbf{k}(t)$ 定义为：


$$
\mathbf{k}(t) = \frac{d\mathbf{T}(t)}{ds}
$$

其中， $\mathbf{T}(t)$ 是单位切向量， $s$ 是弧长参数。

曲率

曲率（Curvature）是曲线在某一点的弯曲程度的量度，是曲率向量的模。

曲率 $\kappa$ 描述曲线在某一点的弯曲程度，其定义为曲率向量的模长：


$$
\kappa = \left| \frac{d\mathbf{T}}{ds} \right|
$$

曲率越大，曲线在该点的弯曲程度越高。对于平面曲线，曲率的倒数称为曲线的半径（Radius of Curvature）。

对于平面曲线，曲率 $\kappa$ 可以通过以下公式计算：


$$
\kappa = \left| \frac{d\mathbf{T}(t)}{ds} \right|
$$

对于参数曲线 $\mathbf{r}(t)$ ，曲率的计算公式为：


$$
\kappa = \frac{\left| \mathbf{r}'(t) \times \mathbf{r}''(t) \right|}{\left| \mathbf{r}'(t) \right|^3}
$$

这里 $\mathbf{r}'(t)$ 和 $\mathbf{r}''(t)$ 分别是曲线的第一和第二导数， $\times$ 表示向量叉积。

曲率向量和曲率的关系

曲率向量 $\mathbf{k}(t)$ 的方向是曲线的法向方向，其大小是曲率 $\kappa$ 。即：


$$
\mathbf{k}(t) = \kappa \mathbf{N}(t)
$$

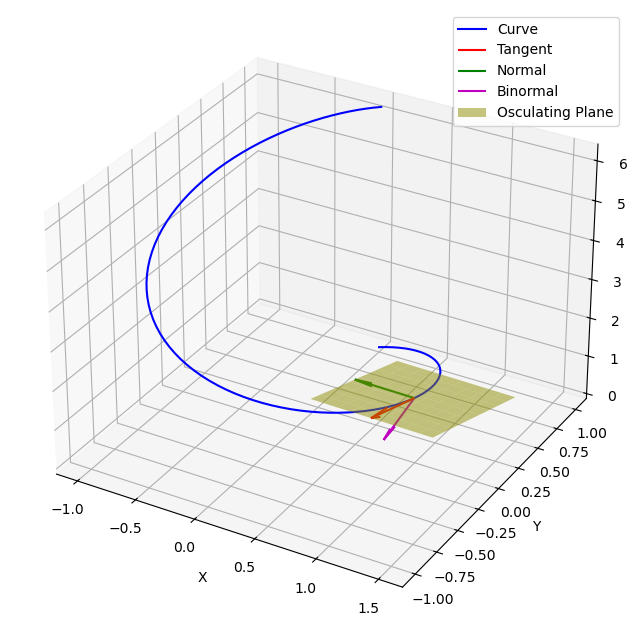
密切平面（Osculating Plane）

密切平面是曲线在某一点处最接近的平面。具体来说，对于空间中的一条光滑曲线，在曲线上的某一点处，密切平面是由该点的切向量和法向量所张成的平面。

切向量（Tangent Vector）：曲线在某一点的切向量是曲线在该点的瞬时方向。可以通过曲线的导数来确定。
法向量（Normal Vector）：法向量是垂直于切向量的向量，指示曲线在该点的曲率方向。

密切平面由这两个向量（切向量和法向量）共同决定。

下面的例子是螺旋线，参数方程：


$$
\begin{cases}
x = \sin(t) \\
y = \cos(t) \\
z = t
\end{cases}
$$

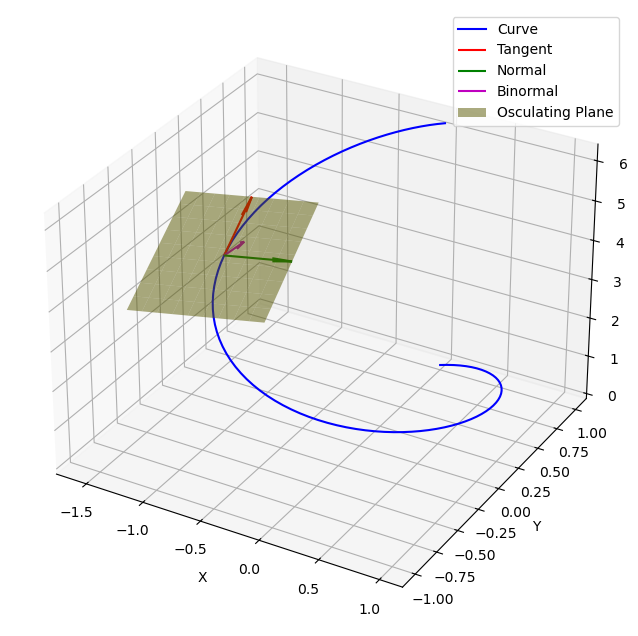
gh|500

副法向量（Binormal Vector）

副法向量是密切平面内垂直于切向量和法向量的向量。它可以通过切向量和法向量的叉乘来确定。

定义：副法向量 $\mathbf{B}$ 是切向量 $\mathbf{T}$ 和法向量 $\mathbf{N}$ 的叉乘结果：
```
$$
\mathbf{B} = \mathbf{T} \times \mathbf{N}
$$
```
- 性质：副法向量、切向量和法向量组成了一个正交的右手坐标系。

挠率（Torsion）

挠率 $\tau$ 描述空间曲线在弯曲过程中扭转的程度，具体来说，挠率量化了曲线的密切平面在曲线沿着切向量方向移动时的旋转速度。其定义为法向量与副法向量之间的变化率：


$$
\tau = -\mathbf{B} \cdot \frac{d\mathbf{N}}{ds}
$$

或者


$$
  \tau = -\frac{d\mathbf{B}}{ds} \cdot \mathbf{N}
$$

挠率衡量曲线从其切平面沿着副法向量方向的扭转程度。如果挠率为零，曲线位于一个平面内，称为平面曲线。如果挠率为零，曲线在该点附近是平面的（没有扭曲）；如果挠率不为零，曲线在该点附近是空间的（有扭曲）。

Frenet-Serret公式

Frenet-Serret公式描述了空间曲线的切向量、法向量和副法向量随弧长变化的规律，是微分几何中的基本公式。这组公式由三条一阶微分方程组成，具体形式如下：


$$
\frac{d\mathbf{T}}{ds} = \kappa \mathbf{N}
$$


$$
\frac{d\mathbf{N}}{ds} = -\kappa \mathbf{T} + \tau \mathbf{B}
$$


$$
\frac{d\mathbf{B}}{ds} = -\tau \mathbf{N}
$$

各方程的意义：

第一方程： 切向量的变化率方向与法向量一致，变化率的大小由曲率决定。
第二方程： 法向量的变化不仅受曲率影响，还受到挠率的影响，通过副法向量表现出来。
第三方程： 副法向量的变化仅由挠率控制，方向与法向量相关。

参数形式


$$
\kappa(t) = ||\mathbf{T}'(t)|| / ||\mathbf{r}'(t)||
$$


$$
\tau(t) = \frac{\det(\mathbf{r}'(t), \mathbf{r}''(t), \mathbf{r}'''(t))}{||\mathbf{T}'(t) \times \mathbf{T}''(t)||^2}
$$

示例：

考虑三维螺旋线：


$$
\mathbf{r}(t) = \begin{pmatrix}
a \cos t \\
a \sin t \\
bt
\end{pmatrix}, \quad t \in \mathbb{R}
$$

其中， $a$ 和 $b$ 为常数，控制螺旋线的半径和垂直间距。

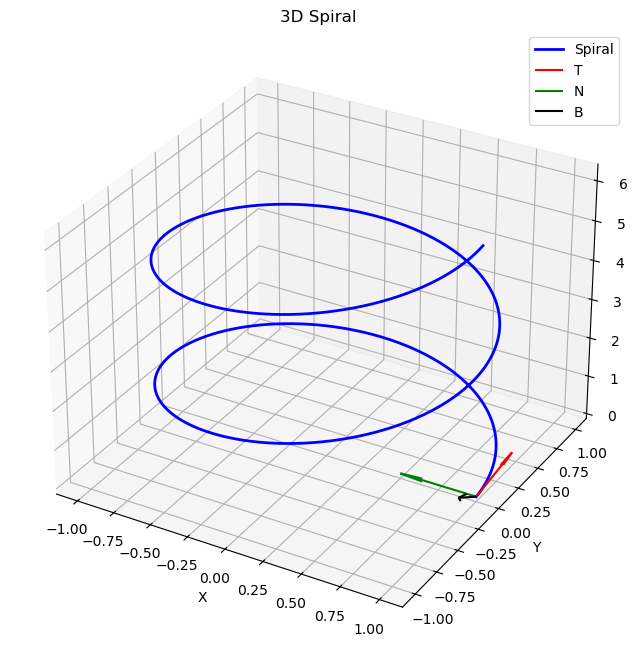
切向量 $\mathbf{T}(t)$ 为位置向量的单位导数，即：


$$
\mathbf{T}(t) = \frac{\mathbf{r}'(t)}{||\mathbf{r}'(t)||}
$$

首先计算 $\mathbf{r}'(t)$ ：


$$
\mathbf{r}'(t) = \frac{d}{dt} \mathbf{r}(t) = \begin{pmatrix}
- a \sin t \\
a \cos t \\
b
\end{pmatrix}
$$

接着计算其模长：


$$
||\mathbf{r}'(t)|| = \sqrt{(-a \sin t)^2 + (a \cos t)^2 + b^2} = \sqrt{a^2 (\sin^2 t + \cos^2 t) + b^2} = \sqrt{a^2 + b^2}
$$

因此，切向量为：


$$
\mathbf{T}(t) = \frac{1}{\sqrt{a^2 + b^2}} \begin{pmatrix}
- a \sin t \\
a \cos t \\
b
\end{pmatrix}
$$

法向量 $\mathbf{N}(t)$ 定义为切向量关于参数 $t$ 的导数单位化：


$$
\mathbf{N}(t) = \frac{\mathbf{T}'(t)}{||\mathbf{T}'(t)||}
$$

首先计算 $\mathbf{T}'(t)$ ：


$$
\mathbf{T}'(t) = \frac{d}{dt} \mathbf{T}(t) = \frac{1}{\sqrt{a^2 + b^2}} \begin{pmatrix}
- a \cos t \\
- a \sin t \\
0
\end{pmatrix}
$$

其模长为：


$$
||\mathbf{T}'(t)|| = \frac{a}{\sqrt{a^2 + b^2}} \sqrt{\cos^2 t + \sin^2 t} = \frac{a}{\sqrt{a^2 + b^2}}
$$

因此，法向量为：


$$
\mathbf{N}(t) = \frac{1}{\frac{a}{\sqrt{a^2 + b^2}}} \cdot \frac{1}{\sqrt{a^2 + b^2}} \begin{pmatrix}
- a \cos t \\
- a \sin t \\
0
\end{pmatrix} = \begin{pmatrix}
- \cos t \\
- \sin t \\
0
\end{pmatrix}
$$

副法向量 $\mathbf{B}(t)$ 为切向量与法向量的叉积：


$$
\mathbf{B}(t) = \mathbf{T}(t) \times \mathbf{N}(t)
$$

计算叉积：


$$
\mathbf{B}(t) = \frac{1}{\sqrt{a^2 + b^2}} \begin{pmatrix}
- a \sin t \\
a \cos t \\
b
\end{pmatrix} \times \begin{pmatrix}
- \cos t \\
- \sin t \\
0
\end{pmatrix}
$$

展开计算：


$$
\mathbf{B}(t) = \frac{1}{\sqrt{a^2 + b^2}} \begin{pmatrix}
(a \cos t)(0) - (b)(- \sin t) \\
(b)(- \cos t) - (- a \sin t)(0) \\
(- a \sin t)(- \sin t) - (a \cos t)(- \cos t)
\end{pmatrix} = \frac{1}{\sqrt{a^2 + b^2}} \begin{pmatrix}
b \sin t \\
- b \cos t \\
a (\sin^2 t + \cos^2 t)
\end{pmatrix}
$$

由于 $\sin^2 t + \cos^2 t = 1$ ，因此：


$$
\mathbf{B}(t) = \frac{1}{\sqrt{a^2 + b^2}} \begin{pmatrix}
b \sin t \\
- b \cos t \\
a
\end{pmatrix}
$$

对于螺旋线，我们可以利用已知的切向量和法向量的关系简化曲率和挠率的计算。

实际上，对于标准的螺旋线，曲率和挠率为常数：


$$
\kappa = \frac{a}{a^2 + b^2}
$$


$$
\tau = \frac{b}{a^2 + b^2}
$$

其中，曲率 $\kappa$ 表示螺旋线在每一点的弯曲程度，挠率 $\tau$ 表示螺旋线的扭转程度。

几何性质分析

曲率（Curvature $\kappa$ ）：曲率越大，螺旋线在该点的弯曲程度越高。对于本螺旋线，曲率 $\kappa = \frac{a}{a^2 + b^2}$ ，当半径 $a$ 增大或垂直间距 $b$ 减小时，曲率增大，螺旋线更加弯曲。
挠率（Torsion $\tau$ ）：挠率越大，螺旋线的扭转程度越高。对于本螺旋线，挠率 $\tau = \frac{b}{a^2 + b^2}$ ，当垂直间距 $b$ 增大或半径 $a$ 减小时，挠率增大，螺旋线更加扭曲。
副法向量（Binormal Vector $\mathbf{B}(t)$ ）：副法向量指向螺旋线的外侧，与切向量和法向量构成右手坐标系，体现了螺旋线在三维空间中的扭转方向。

线积分

线积分（Line Integral）是沿着某条曲线对函数进行积分的过程。在物理学中，线积分广泛应用于计算沿路径的物理量累积，如路径长度、功等。

标量场的线积分

在标量场（Scalar Field）中，线积分用于计算沿着曲线的函数值的累积。

线积分的定义与计算方法

定义：设 $C$ 是参数化为 $\mathbf{r}(t) = (x(t), y(t), z(t))$ ， $t \in [a, b]$ 的光滑曲线， $f: \mathbb{R}^3 \rightarrow \mathbb{R}$ 是定义在 $C$ 上的标量场。标量场 $f$ 沿曲线 $C$ 的线积分定义为：


$$
\int_C f \, ds = \int_a^b f(\mathbf{r}(t)) \|\mathbf{r}'(t)\| \, dt
$$

其中， $ds = \|\mathbf{r}'(t)\| \, dt$ 表示曲线上的微元弧长。

计算方法：

确定曲线 $C$ 的参数化表达式 $\mathbf{r}(t)$ ， $t \in [a, b]$ 。
计算 $\mathbf{r}'(t) = \frac{d\mathbf{r}(t)}{dt}$ 。
计算 $\|\mathbf{r}'(t)\|$ 。
代入积分公式，计算定积分。

应用例子：路径积分

例题：计算曲线 $C$ 上函数 $f(x, y, z) = x^2 + y^2 + z^2$ 的线积分，其中 $C$ 是从点 $(0, 0, 0)$ 沿 $x$ -轴到点 $(1, 0, 0)$ 的直线段。

解答：

参数化曲线 $C$ ： $\mathbf{r}(t) = (t, 0, 0)$ ，其中 $t \in [0, 1]$ 。
计算导数： $\mathbf{r}'(t) = (1, 0, 0)$ ，所以 $\|\mathbf{r}'(t)\| = 1$ 。
计算函数 $f$ 在 $C$ 上的值： $f(\mathbf{r}(t)) = t^2 + 0 + 0 = t^2$ 。
计算积分：


$$
\int_C f \, ds = \int_0^1 t^2 \cdot 1 \, dt = \left[ \frac{t^3}{3} \right]_0^1 = \frac{1}{3}
$$

向量场的线积分

在向量场（Vector Field）中，线积分用于计算沿着曲线方向上的向量场分量的累积，常用于物理中的功（Work）计算。

线积分的定义与计算方法

定义：设 $C$ 是参数化为 $\mathbf{r}(t) = (x(t), y(t), z(t))$ ， $t \in [a, b]$ 的光滑曲线， $\mathbf{F}: \mathbb{R}^3 \rightarrow \mathbb{R}^3$ 是定义在 $C$ 上的向量场。向量场 $\mathbf{F}$ 沿曲线 $C$ 的线积分定义为：


$$
\int_C \mathbf{F} \cdot d\mathbf{r} = \int_a^b \mathbf{F}(\mathbf{r}(t)) \cdot \mathbf{r}'(t) \, dt
$$

其中， $d\mathbf{r} = \mathbf{r}'(t) \, dt$ 是曲线上的微元位移向量。

计算方法：

确定曲线 $C$ 的参数化表达式 $\mathbf{r}(t)$ ， $t \in [a, b]$ 。
计算 $\mathbf{r}'(t) = \frac{d\mathbf{r}(t)}{dt}$ 。
计算向量场 $\mathbf{F}(\mathbf{r}(t))$ 。
计算点积 $\mathbf{F}(\mathbf{r}(t)) \cdot \mathbf{r}'(t)$ 。
代入积分公式，计算定积分。

应用例子：功的计算

例题：在重力场 $\mathbf{F} = (0, -mg, 0)$ （其中 $m$ 为质量， $g$ 为重力加速度）中，将物体从点 $(0, 0, 0)$ 沿曲线 $C$ 移动到点 $(0, h, 0)$ ，计算所做的功。

解答：

参数化曲线 $C$ ：假设沿 $y$ -轴直线运动， $\mathbf{r}(t) = (0, t, 0)$ ，其中 $t \in [0, h]$ 。
计算导数： $\mathbf{r}'(t) = (0, 1, 0)$ 。
计算向量场 $\mathbf{F}(\mathbf{r}(t)) = (0, -mg, 0)$ 。
计算点积：


$$
\mathbf{F} \cdot \mathbf{r}'(t) = (0)(0) + (-mg)(1) + (0)(0) = -mg
$$

计算积分：


$$
\int_C \mathbf{F} \cdot d\mathbf{r} = \int_0^h (-mg) \, dt = -mg \cdot h
$$

结果：所做的功为 $-mgh$ 。

曲面积分

曲面积分（Surface Integral）是对定义在曲面上的函数或向量场进行积分的过程。在物理学中，曲面积分用于计算通过曲面的物理量累积，如流量（Flux）、电磁场等。

面积元

标量面积元

标量面积元用于描述微小面积的大小，即该面积片段的面积量。其表达式为：


$$
dA = \|\mathbf{r}_u \times \mathbf{r}_v\| \, du \, dv
$$

其中：

$\mathbf{r}(u, v)$ 是参数化曲面在参数 $u$ 和 $v$ 下的位置矢量。
$\mathbf{r}_u = \frac{\partial \mathbf{r}}{\partial u}$ 和 $\mathbf{r}_v = \frac{\partial \mathbf{r}}{\partial v}$ 分别是曲面在参数 $u$ 和 $v$ 方向的切矢量。
$\mathbf{r}_u \times \mathbf{r}_v$ 是切矢量的叉积（cross product），其模长 $\|\mathbf{r}_u \times \mathbf{r}_v\|$ 给出了平行四边形的面积，即微小面积片段的绝对面积。

向量面积元

向量面积元不仅包含面积的大小，还包含该面积片段的方向信息。其表达式为：


$$
d\mathbf{S} = \left( \frac{\partial \mathbf{r}}{\partial u} \times \frac{\partial \mathbf{r}}{\partial v} \right) du dv
$$

这里：

$\frac{\partial \mathbf{r}}{\partial u} \times \frac{\partial \mathbf{r}}{\partial v}$ 不仅提供了面积的大小（即标量面积元的模长），还提供了一个法向量（normal vector）方向，表明面积片段的朝向。

标量场的曲面积分

在标量场中，曲面积分用于计算定义在曲面上的标量函数的累积，常用于计算表面积或质量等物理量。

曲面积分的定义与计算方法

定义：设 $S$ 是参数化为 $\mathbf{r}(u, v) = (x(u, v), y(u, v), z(u, v))$ 的光滑曲面， $(u, v)$ 属于参数域 $D \subset \mathbb{R}^2$ ， $f: \mathbb{R}^3 \rightarrow \mathbb{R}$ 是定义在 $S$ 上的标量场。标量场 $f$ 在曲面 $S$ 上的曲面积分定义为：


$$
\iint_S f \, dS = \iint_D f(\mathbf{r}(u, v)) \| \mathbf{r}_u \times \mathbf{r}_v \| \, du \, dv
$$

其中， $dS = \| \mathbf{r}_u \times \mathbf{r}_v \| \, du \, dv$ 表示曲面上的微元面积。

计算方法：

确定曲面 $S$ 的参数化表达式 $\mathbf{r}(u, v)$ ， $(u, v) \in D$ 。
计算偏导数 $\mathbf{r}_u = \frac{\partial \mathbf{r}}{\partial u}$ 、 $\mathbf{r}_v = \frac{\partial \mathbf{r}}{\partial v}$ 。
计算叉积 $\mathbf{r}_u \times \mathbf{r}_v$ 及其模长。
代入积分公式，计算二重积分。

应用例子：表面积的计算

例题：计算单位圆 $x^2 + y^2 = 1$ 在 $xy$ -平面上的表面积。

解答：

参数化曲面：由于是 $xy$ -平面上的曲线向上生成的曲面，可以表述为 $\mathbf{r}(x, y) = (x, y, 0)$ ，其中 $x^2 + y^2 \leq 1$ 。
计算偏导数：


$$
\mathbf{r}_x = (1, 0, 0), \quad \mathbf{r}_y = (0, 1, 0)
$$

计算叉积及模长：


$$
\mathbf{r}_x \times \mathbf{r}_y = (0, 0, 1), \quad \| \mathbf{r}_x \times \mathbf{r}_y \| = 1
$$

计算积分：


$$
\iint_S dS = \iint_D 1 \, dx \, dy
$$

这是单位圆的面积，结果为：


$$
\iint_S dS = \pi \cdot 1^2 = \pi
$$

结果：单位圆在 $xy$ -平面上的表面积为 $\pi$ 。

向量场的曲面积分

在向量场中，曲面积分用于计算通过曲面的向量场分量的累积，通常用于描述流体的流量（Flux）等物理现象。即一个向量场通过一个曲面或边界的“流动”量。例如，电磁学中电场通过一个闭合曲面的通量，或者流体力学中流体速度场通过某一边界的流量。

形式上，对于向量场 $\mathbf{F}$ 和曲面 $S$ ，流量积分定义为：


$$
\iint_S \mathbf{F} \cdot \mathbf{n} \, dS
$$

这里， $\mathbf{F} \cdot \mathbf{n}$ 表示向量场 $\mathbf{F}$ 在法向量方向上的分量，反映了 $\mathbf{F}$ 通过曲面 $S$ 的“有效流量”。也可以写为


$$
\iint_S \mathbf{F} \cdot \, d\mathbf{S}
$$

后面不再区分这两种写法。

流量积分

定义：设 $S$ 是参数化为 $\mathbf{r}(u, v) = (x(u, v), y(u, v), z(u, v))$ 的光滑曲面， $(u, v)$ 属于参数域 $D \subset \mathbb{R}^2$ ， $\mathbf{F}: \mathbb{R}^3 \rightarrow \mathbb{R}^3$ 是定义在 $S$ 上的向量场。向量场 $\mathbf{F}$ 在曲面 $S$ 上的曲面积分定义为：


$$
\iint_S \mathbf{F} \cdot d\mathbf{S} = \iint_D \mathbf{F}(\mathbf{r}(u, v)) \cdot (\mathbf{r}_u \times \mathbf{r}_v) \, du \, dv
$$

其中， $d\mathbf{S} = \mathbf{n} \, dS$ ， $\mathbf{n}$ 为曲面的单位法向量， $dS = \| \mathbf{r}_u \times \mathbf{r}_v \| \, du \, dv$ 。

计算方法：

确定曲面 $S$ 的参数化表达式 $\mathbf{r}(u, v)$ ， $(u, v) \in D$ 。
计算偏导数 $\mathbf{r}_u = \frac{\partial \mathbf{r}}{\partial u}$ 、 $\mathbf{r}_v = \frac{\partial \mathbf{r}}{\partial v}$ 。
计算叉积 $\mathbf{r}_u \times \mathbf{r}_v$ 。
计算点积 $\mathbf{F}(\mathbf{r}(u, v)) \cdot (\mathbf{r}_u \times \mathbf{r}_v)$ 。
代入积分公式，计算二重积分。

解释

假设曲面 $S$ 可以用参数 $u$ 和 $v$ 来参数化，即通过向量函数 $\mathbf{r}(u, v)$ 将参数域 $D$ 映射到曲面 $S$ 上：


$$
\mathbf{r}: D \rightarrow S
$$

在参数域 $D$ 上的一个小矩形面积元 $du \, dv$ ，在曲面 $S$ 上对应的面元是一个平行四边形，其边由 $\mathbf{r}_u$ 和 $\mathbf{r}_v$ 表示：


$$
\mathbf{r}_u = \frac{\partial \mathbf{r}}{\partial u}, \quad \mathbf{r}_v = \frac{\partial \mathbf{r}}{\partial v}
$$

这个平行四边形的面积元向量可以表示为（回忆叉乘的定义：平行四边形的有向面积）：


$$
d\mathbf{S} = (\mathbf{r}_u \times \mathbf{r}_v) \, du \, dv
$$

向量场 $\mathbf{F}$ 在曲面 $S$ 上的通量可以表示为：


$$
\iint_S \mathbf{F} \cdot d\mathbf{S}
$$

将 $d\mathbf{S}$ 替换为其参数化形式：


$$
d\mathbf{S} = (\mathbf{r}_u \times \mathbf{r}_v) \, du \, dv
$$

因此，通量积分可以写成：


$$
\iint_S \mathbf{F} \cdot d\mathbf{S} = \iint_S \mathbf{F} \cdot (\mathbf{r}_u \times \mathbf{r}_v) \, du \, dv
$$

在参数域 $D$ 上进行积分时，向量场 $\mathbf{F}$ 需要在曲面上的点 $\mathbf{r}(u, v)$ 处进行评估：


$$
\mathbf{F}(\mathbf{r}(u, v))
$$

于是，上述通量积分变为：


$$
\iint_S \mathbf{F} \cdot d\mathbf{S} = \iint_D \mathbf{F}(\mathbf{r}(u, v)) \cdot (\mathbf{r}_u \times \mathbf{r}_v) \, du \, dv
$$

散度与流量

散度 $\nabla \cdot \mathbf{F}$ 在某一点处度量的是向量场 $\mathbf{F}$ 在该点的“源强”或“汇强”。具体而言：

如果 $\nabla \cdot \mathbf{F} > 0$ ，表示在该点处有源，向外散发流量。
如果 $\nabla \cdot \mathbf{F} < 0$ ，表示在该点处有汇，流量向内聚集。
若 $\nabla \cdot \mathbf{F} = 0$ ，表明该点处没有净流出或流入，向量场是无源的。

散度定理将整个区域内的散度（源汇强度的积累）与通过其边界的总流量联系起来。

应用例子：流量的计算

例题：在向量场 $\mathbf{F} = (yz, xz, xy)$ 中，计算通过单位球面 $S$ （半径为 1，中心在原点）的流量。

解答：

使用球坐标参数化单位球面：


$$
\mathbf{r}(\theta, \phi) = (\sin\theta \cos\phi, \sin\theta \sin\phi, \cos\theta)
$$

其中， $\theta \in [0, \pi]$ ， $\phi \in [0, 2\pi]$ 。

计算偏导数：


$$
\mathbf{r}_\theta = (\cos\theta \cos\phi, \cos\theta \sin\phi, -\sin\theta)
$$


$$
\mathbf{r}_\phi = (-\sin\theta \sin\phi, \sin\theta \cos\phi, 0)
$$

计算叉积：


$$
\mathbf{r}_\theta \times \mathbf{r}_\phi = (\sin^2\theta \cos\phi, \sin^2\theta \sin\phi, \sin\theta \cos\theta)
$$

计算点积 $\mathbf{F} \cdot (\mathbf{r}_\theta \times \mathbf{r}_\phi)$ ：


$$
\mathbf{F}(\mathbf{r}(\theta, \phi)) = (yz, xz, xy) = (\sin\theta \sin\phi \cos\theta, \sin\theta \cos\phi \cos\theta, \sin^2\theta \cos\phi \sin\phi)
$$


$$
\mathbf{F} \cdot (\mathbf{r}_\theta \times \mathbf{r}_\phi) = (\sin\theta \sin\phi \cos\theta)(\sin^2\theta \cos\phi) + (\sin\theta \cos\phi \cos\theta)(\sin^2\theta \sin\phi) + (\sin^2\theta \cos\phi \sin\phi)(\sin\theta \cos\theta)
$$

化简后得到：


$$
\mathbf{F} \cdot (\mathbf{r}_\theta \times \mathbf{r}_\phi) = \sin^3\theta \cos\theta \sin\phi \cos\phi + \sin^3\theta \cos\theta \sin\phi \cos\phi + \sin^3\theta \cos\theta \sin\phi \cos\phi = 3 \sin^3\theta \cos\theta \sin\phi \cos\phi
$$

计算积分：

由于被积函数关于 $\phi$ 为奇函数，积分在 $\phi \in [0, 2\pi]$ 上为零。因此，流量为零。

结果：通过单位球面的流量为 0。

在多变量微积分和理论物理中，积分定理（Integral Theorems）是连接微分运算与积分运算的重要桥梁。它们在解析物理现象、简化计算以及建立基本定律中起着关键作用。本章节将详细介绍三大经典积分定理：格林定理（Green’s Theorem）、斯托克斯定理（Stokes’ Theorem）以及散度定理（Divergence Theorem，又称高斯定理）。每个定理将涵盖其陈述、证明以及在物理中的应用，以帮助读者全面理解其理论基础和实际意义。

牛顿-莱布尼兹定理

让我们回顾这一定理：

如果函数 $f(x)$ 在区间 $[a, b]$ 上是连续的，并且 $F(x)$ 是 $f(x)$ 的一个原函数（即 $F'(x) = f(x)$ ），那么：


$$
   \int_a^b f(x) \, dx = F(b) - F(a)
$$

这部分表明，定积分可以通过原函数的的两个点来计算。

格林定理

格林定理的陈述

请观看视频：https://www.bilibili.com/video/BV1dg4y1v7RP

格林定理是平面上的一个基本积分定理，它将曲线积分与区域内的二重积分联系起来。具体来说，设 $C$ 是平面上一个简单、光滑且正向取向（逆时针）的闭合曲线， $D$ 是由 $C$ 所围成的有界区域。若 $P(x, y)$ 和 $Q(x, y)$ 在 $D$ 上具有连续的偏导数，分别是向量场 $\mathbf{F}$ 的 $x$ 分量和 $y$ 分量。则


$$
\oint_{C} \left( P \, dx + Q \, dy \right) = \iint_{D} \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA
$$

格林定理的旋度形式可以记为：


$$
\oint_C \mathbf{F} \cdot d\mathbf{r}  = \iint_D \nabla \times \mathbf{F} \, d\mathbf{A}
$$

称为斯托克斯定理，其中：

$\mathbf{F} = (P, Q)$ 是一个在 $D$ 上具有连续偏导数的向量场。
$\oint_C \mathbf{F} \cdot d\mathbf{r}$ 表示沿曲线 $C$ 的线积分。
$\nabla \times \mathbf{F}$ 是向量场 $\mathbf{F}$ 的旋度。

格林定理可以被看作是二维情况下的散度定理。它表明，围绕一个区域的曲线积分等于该区域内部的某种“旋转”或“涡度”的总和。直观上，可以想象成区域内的“旋转”如何通过边界流出。

这表明，可以用二维区域内部的信息计算沿边界的曲线积分。这与牛顿-莱布尼兹定理存在直觉上的同构性。

格林定理的应用

平面区域的面积计算

格林定理不仅限于向量场的积分，还可以用来简便地计算平面区域的面积。设 $C$ 为平面上一个简单闭合曲线，正向取向，则区域 $D$ 的面积 $A$ 可表示为：


$$
A = \frac{1}{2} \oint_{C} \left( x \, dy - y \, dx \right)
$$

证明与推导：

利用格林定理，对于 $P = -\frac{y}{2}$ ， $Q = \frac{x}{2}$ ，有


$$
\oint_{C} \left( P \, dx + Q \, dy \right) = \iint_{D} \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA = \iint_{D} \left( \frac{1}{2} + \frac{1}{2} \right) dA = \iint_{D} dA = A
$$

所以，


$$
A = \frac{1}{2} \oint_{C} \left( x \, dy - y \, dx \right)
$$

实例：

计算单位圆 $C$ 的面积：

参数化 $C$ 为 $x = \cos\theta$ , $y = \sin\theta$ , $\theta \in [0, 2\pi]$ 。


$$
A = \frac{1}{2} \oint_{C} \left( \cos\theta \, d(\sin\theta) - \sin\theta \, d(\cos\theta) \right) = \frac{1}{2} \int_{0}^{2\pi} \left( \cos\theta \cdot \cos\theta \, d\theta + \sin^2\theta \, d\theta \right) = \frac{1}{2} \int_{0}^{2\pi} d\theta = \pi
$$

这与已知单位圆的面积 $\pi$ 一致。

散度定理（高斯定理）

请看视频：The Divergence Theorem, a visual explanation - YouTube

散度定理的陈述

设 $V$ 是三维空间中的有界区域， $\mathbf{F}$ 是定义在 $V$ 上的向量场，并且其分量具有连续的一阶偏导数。设 $\partial V$ 为 $V$ 的边界（一个光滑的闭合曲面）， $\mathbf{n}$ 是边界曲面上的单位外法向量，则


$$
\iiint_{V} (\nabla \cdot \mathbf{F}) \, dV = \iint_{\partial V} \mathbf{F} \cdot \mathbf{n} \, dS
$$

其中， $\nabla \cdot \mathbf{F}$ 表示 $\mathbf{F}$ 的散度， $dV$ 是体积元， $dS$ 是曲面元。

直观理解

散度定理揭示了一个局部性质与整体性质之间的联系：

局部性质：向量场 $\mathbf{F}$ 在每一点的散度 $\nabla \cdot \mathbf{F}$ 描述了该点的源汇特性。
整体性质：通过整个边界 $\partial V$ 的总流量，是所有局部散度在整个区域上的积分。

因此，散度定理可视为“局部性质的累积等于整体效应”的一种体现。

设想一个封闭的气球（区域 $V$ ）以及其表面（边界 $\partial V$ ）。向量场 $\mathbf{F}$ 可以代表气体的速度场。

散度 $\nabla \cdot \mathbf{F}$ ：在气球内的每一点，散度表示气体是否在该点有净流出的趋势（如有新气体注入，产生正散度）或净流入的趋势（如气体被消耗，产生负散度）。
总流量 $\iint_{\partial V} \mathbf{F} \cdot \mathbf{n} \, dS$ ：整个气球表面上气体通过表面的总量。如气球内部不断有气体流出，表面总流量即为气体流出气球的速率。

散度定理说明，气球内部所有点的净流出速率（散度的体积分）恰好等于气球表面上气体的总流出速率（流量的表面积分）。这是一种量化“源汇”与“整体流动”之间平衡关系的数学表达。

为了更深入理解，可以将区域 $V$ 分割成许多小的子区域 $\Delta V_i$ ，每个子区域的边界部分与相邻子区域公共的内部面上的流量抵消，仅剩下整个 $V$ 的边界 $\partial V$ 上的流量。

通过对所有子区域应用流量的局部平衡（即微元体积内的散度等于流量的净变化），并在极限情况下取无限小体积，最终得到整个区域的流量与散度的体积分相等的结论。

散度定理在物理中的应用

高斯定律

散度定理在电磁学中用于描述电场与电荷分布的关系，称为高斯定律。高斯定律指出，封闭曲面上的电场通量等于该曲面内部的总电荷量与真空介电常数的比值。数学表达式为：


$$
\iiint_V (\nabla \cdot \mathbf{E}) \, dV = \iint_{\partial V} \mathbf{E} \cdot \mathbf{n} \, dS = \frac{Q_{\text{enc}}}{\varepsilon_0}
$$

这里， $Q_{\text{enc}}$ 是区域 $V$ 内的总电荷量， $\varepsilon_0$ 是真空介电常数。散度定理将电场的涌出与电荷的分布联系起来，体现了电荷是电场的源。

利用散度定理，可将其转化为微分形式：


$$
\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}
$$

其中， $\rho$ 是电荷密度。这表明电场的强弱与电荷密度的线性关系。

实例：

计算一个半径为 $R$ 的均匀带电球体外部的电场。

选取高斯面：选择半径为 $r > R$ 的球面对称的高斯面。
应用高斯定律：


$$
\iint_{S} \mathbf{E} \cdot d\mathbf{S} = E(r) \cdot 4\pi r^2 = \frac{Q}{\varepsilon_0}
$$

其中， $Q$ 是球体的总电荷量。

解得电场：


$$
E(r) = \frac{Q}{4\pi \varepsilon_0 r^2}
$$

这与库仑定律一致，表明散度定理在电场计算中的有效性。

广义斯托克斯定理

定理描述

设 $M$ 是一个带边界的光滑 $k$ -维流形， $\partial M$ 是其边界， $\omega$ 是一个定义在 $M$ 上的 $(k-1)$ -形式。那么广义斯托克斯定理表述为：


$$
\int_M d\omega = \int_{\partial M} \omega
$$

其中， $d\omega$ 是 $\omega$ 的外微分。

积分定理的统一

广义斯托克斯定理可以统一多个经典积分定理：

格林定理：在二维平面上，将区域 $D$ 和其边界 $\partial D$ 的曲线积分与面积分联系起来。


$$
\oint_{\partial D} (P \, dx + Q \, dy) = \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA
$$

斯托克斯定理：在三维空间中，将曲面 $S$ 和其边界 $\partial S$ 的曲线积分与曲面积分联系起来。
```
$$
\oint_{\partial S} \mathbf{F} \cdot d\mathbf{r} = \iint_S (\nabla \times \mathbf{F}) \cdot d\mathbf{S}
$$
```
散度定理（高斯定理）：在三维空间中，将体积 $V$ 和其边界 $\partial V$ 的曲面积分与体积分联系起来。
```
$$
\iint_{\partial V} \mathbf{F} \cdot d\mathbf{S} = \iiint_V (\nabla \cdot \mathbf{F}) dV
$$
```

微分形式与外微分

微分形式的定义与基本性质

微分形式的定义

在 $n$ -维光滑流形 $M$ 上， $k$ -次微分形式（ $k$ -form）是一种光滑的反对称张量场。具体来说， $k$ -形式是 $k$ 个切向量场的反对称多线性映射。更形式化地， $k$ -形式属于外微分代数（Exterior Algebra）的第 $k$ 阶部分，记作 $\Omega^k(M)$ 。

定义：设 $M$ 是一个 $n$ 维光滑流形， $p \in M$ ，则在 $p$ 处的 $k$ -形式 $\omega_p$ 是切空间 $T_pM$ 上的 $k$ -次反对称双线性映射：


$$
\omega_p: \underbrace{T_pM \times T_pM \times \cdots \times T_pM}_{k\,\text{times}} \to \mathbb{R}
$$

满足以下反对称性：


$$
\omega_p(v_{\sigma(1)}, v_{\sigma(2)}, \ldots, v_{\sigma(k)}) = \text{sign}(\sigma) \omega_p(v_1, v_2, \ldots, v_k)
$$

其中， $\sigma$ 是 $k$ 阶置换， $\text{sign}(\sigma)$ 是其符号。

微分形式可以被看作是对向量场的线性泛函，能够在不同的流形（Manifold）上进行积分。它们是外微分代数（Exterior Algebra）的元素，能够通过外积（Exterior Product）进行组合，形成更高阶的形式。

0-形式（0-Form）：在流形上光滑的函数（Smooth Functions）。
1-形式（1-Form）：可以表示为 $\omega = f_1 \, dx^1 + f_2 \, dx^2 + \cdots + f_n \, dx^n$ ，其中 $f_i$ 是光滑函数， $dx^i$ 是坐标的微分。
k-形式（k-Form）：由k个1-形式的外积组成，例如2-形式、3-形式等。

微分形式的一个关键特性是它们可以通过外微分算子（Exterior Derivative）进行操作。外微分将k-形式映射到(k+1)-形式，满足 $d(d\omega) = 0$ 的性质。

基本性质

线性性：微分形式对其每个变量都是线性的。
反对称性：交换任意两个变量会导致符号变化。
局部分解：在坐标图中， $k$ -形式可以表示为基1-形式的外积的线性组合。
外微分运算：微分形式之间存在一种自然的微分运算，称为外微分（Exterior Derivative），将 $k$ -形式映射到 $(k+1)$ -形式。
外代数结构：微分形式构成一个外代数，其乘法为外积（Wedge Product），具备反对称性和结合性。

例子

1-形式的例子

考察二维笛卡尔坐标系中的1-形式：


$$
\omega = P(x, y) \, dx + Q(x, y) \, dy
$$

其中， $P$ 和 $Q$ 是光滑函数。这个1-形式可以用来表示平面上的线积分，例如电场的功或流体的路径积分。

面积的2-形式

在三维空间中，一个简单的2-形式可以表示为：


$$
\omega = f(x, y, z) \, dx \wedge dy
$$

这里， $f(x, y, z)$ 是一个光滑函数， $dx \wedge dy$ 表示 $dx$ 和 $dy$ 的外积（可以将其理解为一个小区域的面积元）。这个2-形式可以用于计算在xy平面上的面积积分。

电磁学中的2-形式

在电磁学中，电场 $\mathbf{E}$ 和磁场 $\mathbf{B}$ 可以被组合成一个电磁张量形式（Electromagnetic Tensor Form）：


$$
F = E_x \, dx \wedge dt + E_y \, dy \wedge dt + E_z \, dz \wedge dt + B_x \, dy \wedge dz + B_y \, dz \wedge dx + B_z \, dx \wedge dy
$$

这里， $dt$ 表示时间的微分， $F$ 是一个2-形式，用于统一描述电场和磁场的性质。

可以简写为向量场和2-形式的组合：


$$
F = \mathbf{E} \wedge dt + \mathbf{B}
$$

这里， $\mathbf{E}$ 和 $\mathbf{B}$ 分别是电场和磁场的向量表示

体积的3-形式

在三维空间中，体积元素可以表示为一个3-形式：


$$
\omega = f(x, y, z) \, dx \wedge dy \wedge dz
$$

这个形式用于计算体积积分，如质量、能量等物理量在空间中的分布。

外微分与外积的计算

外积的定义与性质

外积（Wedge Product）是外代数中的基本运算，将两个微分形式结合生成一个新的微分形式。对于 $k$ -形式 $\alpha$ 和 $l$ -形式 $\beta$ ，它们的外积 $\alpha \wedge \beta$ 是一个 $(k+l)$ -形式，定义为：


$$
(\alpha \wedge \beta)(v_1, v_2, \ldots, v_{k+l}) = \frac{1}{k!l!} \sum_{\sigma \in S_{k+l}} \text{sign}(\sigma) \alpha(v_{\sigma(1)}, \ldots, v_{\sigma(k)}) \beta(v_{\sigma(k+1)}, \ldots, v_{\sigma(k+l)})
$$

性质：

反对称性： $\alpha \wedge \beta = (-1)^{kl} \beta \wedge \alpha$ 。
双线性性：
1. 结合律： $(\alpha \wedge \beta) \wedge \gamma = \alpha \wedge (\beta \wedge \gamma)$ 。
2. 分配律： $\alpha \wedge (\beta + \gamma) = \alpha \wedge \beta + \alpha \wedge \gamma$ 。

外微分的定义与计算

外微分（Exterior Derivative）是将 $k$ -形式映射到 $(k+1)$ -形式的微分运算。设 $\omega$ 是 $k$ -形式，其外微分 $d\omega$ 定义为：


$$
d\omega(v_0, v_1, \ldots, v_k) = \sum_{i=0}^k (-1)^i v_i (\omega(v_0, \ldots, \hat{v}_i, \ldots, v_k)) + \sum_{0 \leq i < j \leq k} (-1)^{i+j} \omega([v_i, v_j], v_0, \ldots, \hat{v}_i, \ldots, \hat{v}_j, \ldots, v_k)
$$

其中， $\hat{v}_i$ 表示省略第 $i$ 个向量， $[v_i, v_j]$ 是向量场的李括号（Lie Bracket）。

性质：

线性性： $d(\alpha + \beta) = d\alpha + d\beta$ 。
幂零性： $d \circ d = 0$ ，即 $d^2 = 0$ 。
莱布尼茨律： $d(\alpha \wedge \beta) = d\alpha \wedge \beta + (-1)^k \alpha \wedge d\beta$ ，其中 $\alpha$ 是 $k$ -形式。

以下通过几个具体例子，介绍外微分的计算和应用。

函数的外微分

考虑一个光滑函数 $f : \mathbb{R}^n \rightarrow \mathbb{R}$ 。

例子 1：设 $f(x, y, z) = x^2 + y^2 + z^2$ 。

外微分计算：

函数 $f$ 的外微分 $df$ 是一个 1-形式，计算如下：


$$
df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy + \frac{\partial f}{\partial z} dz
$$

计算偏导数：


$$
\frac{\partial f}{\partial x} = 2x, \quad \frac{\partial f}{\partial y} = 2y, \quad \frac{\partial f}{\partial z} = 2z
$$

因此，


$$
df = 2x\,dx + 2y\,dy + 2z\,dz
$$

1-形式的外微分

考虑一个 1-形式 $\omega$ 在 $\mathbb{R}^3$ 中的表达式。

例子 2：设 $\omega = P\,dx + Q\,dy + R\,dz$ ，其中 $P, Q, R$ 是光滑函数。

外微分计算：

外微分 $d\omega$ 是一个 2-形式，计算如下：


$$
d\omega = \left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) dy \wedge dz + \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) dz \wedge dx + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dx \wedge dy
$$

具体例子：

设 $\omega = y\,dx + z\,dy + x\,dz$ 。

计算各项偏导数：


$$
\frac{\partial R}{\partial y} = \frac{\partial x}{\partial y} = 0, \quad \frac{\partial Q}{\partial z} = \frac{\partial z}{\partial z} = 1
$$


$$
\frac{\partial P}{\partial z} = \frac{\partial y}{\partial z} = 0, \quad \frac{\partial R}{\partial x} = \frac{\partial x}{\partial x} = 1
$$


$$
\frac{\partial Q}{\partial x} = \frac{\partial z}{\partial x} = 0, \quad \frac{\partial P}{\partial y} = \frac{\partial y}{\partial y} = 1
$$

因此，


$$
d\omega = (0 - 1) dy \wedge dz + (0 - 1) dz \wedge dx + (0 - 1) dx \wedge dy = -dy \wedge dz - dz \wedge dx - dx \wedge dy
$$

2-形式的外微分

外微分操作可以作用于任何阶的微分形式。下面是一个 2-形式的例子。

例子 3：设 $\eta = P\,dx \wedge dy + Q\,dy \wedge dz + R\,dz \wedge dx$ 是一个 2-形式。

外微分计算：

外微分 $d\eta$ 是一个 3-形式，计算如下：


$$
d\eta = \left( \frac{\partial P}{\partial z} + \frac{\partial Q}{\partial x} + \frac{\partial R}{\partial y} \right) dx \wedge dy \wedge dz
$$

具体例子：

设 $\eta = x\,dx \wedge dy + y\,dy \wedge dz + z\,dz \wedge dx$ 。

计算各项偏导数：


$$
\frac{\partial P}{\partial z} = \frac{\partial x}{\partial z} = 0, \quad \frac{\partial Q}{\partial x} = \frac{\partial y}{\partial x} = 0, \quad \frac{\partial R}{\partial y} = \frac{\partial z}{\partial y} = 0
$$

因此，


$$
d\eta = (0 + 0 + 0) dx \wedge dy \wedge dz = 0
$$

例子：磁场强度的外微分为 0

在麦克斯韦方程组中，外微分用于描述电场和磁场的性质。例如，磁场强度 $\mathbf{B}$ 可以表示为一个 2-形式，其外微分为零，即没有磁单极子：


$$
d\mathbf{B} = 0
$$

（如果 $dB = 0$ ，这意味着 2-形式 $B$ 是闭的。根据斯托克斯定理，这等价于说 $\mathbf{B}$ 的散度为零，即 $\nabla \cdot \mathbf{B} = 0$ 。）

微分形式的积分与应用

微分形式的积分为流形上的积分提供了统一的框架。不同类型的积分，如曲线积分、曲面积分以及更高维的积分，都可以通过微分形式的积分来表示。

微分形式的积分

设 $M$ 是一个 $n$ 维光滑定向流形， $\omega$ 是一个 $n$ -形式， $M$ 上的积分定义为：


$$
\int_M \omega
$$

对于低维情况，如1-形式和2-形式，其积分分别对应于曲线上的线积分和曲面上的面积分。

应用

斯托克斯定理：微分形式的积分理论统一了格林公式、高斯定理和经典的斯托克斯定理。具体地，对于一个 $(k-1)$ -形式 $\omega$ ，有：


$$
\int_{\partial M} \omega = \int_M d\omega
$$

电磁学：麦克斯韦方程组可以用微分形式简洁地表示，使得方程具有协变性，便于在不同坐标系下运用。
流形理论：在流形的同调和上同调理论中，微分形式起着核心作用，尤其在德拉姆（de Rham）同调中。

麦克斯韦方程组的微分形式

高斯定律（Gauss’s Law）：


$$
   dD = \rho
$$

高斯磁定律（Gauss’s Law for Magnetism）：


$$
   dB = 0
$$

法拉第电磁感应定律（Faraday’s Law of Induction）：


$$
   dE = -\frac{\partial B}{\partial t}
$$

安培-麦克斯韦定律（Ampère-Maxwell Law）：


$$
   dH = J + \frac{\partial D}{\partial t}
$$

其中，

$H$ 是磁场强度 1-形式，
$J$ 是电流密度 2-形式，
$\rho$ 是电荷密度 3-形式。

向量场的拓扑性质

向量场的奇点与分类

向量场（Vector Fields）是光滑流形上切向量空间的截面，描述了每一点的方向和大小。在研究向量场的拓扑性质时，奇点（Singularities）的分析尤为重要。

奇点的定义与性质

奇点指的是向量场在某一点处取零的点，即该点处向量场不定义方向。奇点的分类依赖于其线性化行为和指数（Index）。

孤立奇点：只有有限多个奇点且每个奇点在其附近区域内唯一。
非孤立奇点：奇点在一条曲线上或更高维的集合中连续分布。

奇点的分类

根据线性化后的行为，奇点通常分为以下几类：

结点（Node）：所有特征值为实数，向量场在奇点附近具有稳定的增长或收缩行为。
鞍点（Saddle Point）：特征值具有不同符号，向量场表现出分支的增长和收缩。
焦点（Focus）：特征值为复数，向量场在奇点附近呈现旋转行为。
中心（Center）：特征值纯虚，向量场在奇点附近呈现周期性闭合轨道。

通过庞加莱（Poincaré）分类，可以更系统地描述奇点的行为。

向量场的霍普夫定理与应用

霍普夫定理（Poincaré-Hopf Theorem）是描述流形上的向量场奇点与流形拓扑性质之间关系的重要结果。

霍普夫定理的表述

设 $M$ 是一个紧致、无界边界的 $n$ 维光滑流形， $\mathcal{V}$ 是 $M$ 上的光滑向量场，且 $\mathcal{V}$ 的奇点都是孤立的，则有：


$$
\sum_{p \in \text{Sing}(\mathcal{V})} \text{Index}(p) = \chi(M)
$$

其中， $\text{Index}(p)$ 是奇点 $p$ 的指数， $\chi(M)$ 是流形 $M$ 的欧拉特征数（Euler Characteristic）。

应用

欧拉特征数的计算：通过构造适当的向量场，可以利用霍普夫定理计算复杂流形的欧拉特征数。
流形的分类：帮助区分不同拓扑类型的流形，如球面与环面的区别。
动力系统：在分析动力系统的稳定性和相图结构时，霍普夫定理提供重要的理论支持。

张量分析

张量的基本概念与运算

张量（Tensors）是多线性代数中的基础概念，广泛应用于物理学和工程学，特别是在描述物理量的多维性质时。

张量的定义

在向量空间 $V$ 及其对偶空间 $V^*$ 上， $k$ -阶协变张量（Covariant Tensor）和 $k$ -阶逆变张量（Contravariant Tensor）的定义分别基于 $V^*$ 和 $V$ 的张量积。

一般情况下，一个 $(r,s)$ 型张量（Tensor of type $(r,s)$ ）是在 $V^*$ 的 $r$ 次张量积和 $V$ 的 $s$ 次张量积上的元素：


$$
T \in V^{*\otimes r} \otimes V^{\otimes s}
$$

张量的运算

张量积（Tensor Product）：将两个张量合成为一个更高阶的张量。
收缩（Contraction）：通过将逆变和协变指标配对并求和，降低张量的阶数。
对称与反对称张量：通过交换指标并应用对称或反对称操作，得到对称张量和反对称张量。

基本性质

多线性性：张量对每个变量都是线性的。
基变换性质：张量的表示在不同基下通过张量积的规则变换。
内积与外积：结合张量的收缩和张量积，构建各种内积和外积结构。

张量场与张量微积分

张量场的定义

在光滑流形 $M$ 上，张量场（Tensor Fields）是每一点处定义一个张量的光滑截面。一个 $(r,s)$ 型张量场 $\mathcal{T}$ 将每个点 $p \in M$ 映射到 $(r,s)$ 型张量 $\mathcal{T}_p$ 属 $T_p^*M^{\otimes r} \otimes T_pM^{\otimes s}$ 。

张量微积分

在张量场上定义微分运算，包括：

协变导数（Covariant Derivative）：在给定联络（Connection）的条件下，对张量场进行微分，保持张量类型不变。
李导数（Lie Derivative）：沿着向量场的流动对张量场进行导数运算，描述张量场的对称性。
外导数（Exterior Derivative）：专门用于微分形式的导数运算，推广到更高阶的张量场。

运算规则

线性性：导数运算对张量场的线性组合保持线性。
莱布尼茨规则：导数运算满足类似乘积规则的莱布尼茨性质。
交换性与结合性：不同类型的导数运算在特定条件下可以交换或结合。

张量在物理中的应用

张量在物理学中起着关键作用，尤其在描述多方向和多尺度的物理现象时。以广义相对论为例，张量分析的应用尤为重要。

广义相对论中的张量

广义相对论（General Relativity）是描述引力的理论，其核心方程——爱因斯坦场方程（Einstein Field Equations）——是关于时空曲率的张量方程。

度规张量（Metric Tensor） $g_{\mu\nu}$ ：描述时空的几何性质，定义了测地线（Geodesics）和距离。
曲率张量（Riemann Curvature Tensor） $R^\rho_{\ \sigma\mu\nu}$ ：刻画时空的曲率，反映引力的本质。
爱因斯坦张量（Einstein Tensor） $G_{\mu\nu}$ ：由曲率张量和度规张量构成，出现在爱因斯坦场方程中。

爱因斯坦场方程

爱因斯坦场方程描述了时空与物质能量分布的关系，形式为：


$$
G_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu}
$$

其中， $G_{\mu\nu}$ 是爱因斯坦张量， $\Lambda$ 是宇宙学常数， $G$ 是引力常数， $c$ 是光速， $T_{\mu\nu}$ 是应力-能量张量（Stress-Energy Tensor），描述物质和能量的分布。

应用与意义

时空曲率与引力：通过度量张量和曲率张量，广义相对论将引力解释为时空的弯曲。
黑洞与宇宙学：爱因斯坦场方程的解包括黑洞（如史瓦西解、克尔解）和宇宙学模型（如弗里德曼–勒梅特–罗伯逊–沃尔克度规）。
引力波：张量分析帮助预测和描述引力波的特性，这些波动是时空曲率的变化，可以通过微分形式进行描述和分析。