回溯算法及其优化
什么是回溯
回溯可以看作在树状的解空间中搜索,一旦发现不可行,就回退到历史状态,然后选择另一个分叉搜索。由于要遍历尝试各个分支,所以也是一种暴力算法。
回溯的标准流程
一般过程:
-
存档
-
执行动作
-
回档
其实就和操作系统的调度、中断啥的一样,保存现场恢复现场。
有的情况下,比如递归实现的后序遍历,可以利用调用栈存档,这样就不用我们显式地存档。
回溯的优化
回溯没有动态规划那么容易进行空间优化,因为 DP 往往能够利用历史状态进行缓存。回溯常用的优化有:
-
交换代替插入删除
-
利用数学性质,无重复优化
-
通过增加条件限制,剪枝优化
全排列
【例子】46. 全排列
对于集合 {1,2,3} 全排列,相当于将 1,2,3 填到三个格子里。
那么对于第一个格子,我们选择填入 ?
-
1
-
2
-
3
这里就产生了三个分支。剩下的两个格子,就是剩余元素的全排列,比如第一个格子填入 3,那么剩下的格子就是 {1,2} 的全排列。
-
历史状态:已经填入的格子。
-
候选集合:剩下能填的数字。
-
对于每个候选元素,都将会产生一个新的候选分支。
参考代码如下:
1class Solution {
2 void rec(vector<int> &available, vector<int> &history,
3 vector<vector<int>> &ret) {
4 if (available.size() == 0) {
5 ret.push_back(history);
6 }
7 // == 尝试各个可用分支 ==
8 for (int i = 0; i < available.size(); i++) {
9 // 存档
10 int num = available[i];
11 history.push_back(num);
12 // 尝试
13 available.erase(available.begin() + i);
14 rec(available, history, ret);
15 // 回档
16 available.insert(available.begin() + i, num);
17 history.pop_back();
18 }
19 }
20
21 public:
22 vector<vector<int>> permute(vector<int> &nums) {
23 vector<vector<int>> ret;
24 vector<int> history;
25 rec(nums, history, ret);
26 return ret;
27 }
28};
你可以注意到,核心代码就这么几句:
1 history.push_back(num);
2 // 尝试
3 available.erase(available.begin() + i);
4 rec(available, history, ret);
5 // 回档
6 available.insert(available.begin() + i, num);
7 history.pop_back();
很有对称美。总之,原来啥样,还原之后就是啥样。
增删性能优化
在时间复杂度上已经很难优化了,因为必须列出所有结果。但是从计算机设计的角度,我们可以减少数组的动态操作。实际上,可以用 swap 代替频繁的数组增删。下面是 LC 提供的题解:
1class Solution {
2public:
3 void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){
4 // 所有数都填完了
5 if (first == len) {
6 res.emplace_back(output);
7 return;
8 }
9 for (int i = first; i < len; ++i) {
10 // 动态维护数组
11 swap(output[i], output[first]);
12 // 继续递归填下一个数
13 backtrack(res, output, first + 1, len);
14 // 撤销操作
15 swap(output[i], output[first]);
16 }
17 }
18 vector<vector<int>> permute(vector<int>& nums) {
19 vector<vector<int> > res;
20 backtrack(res, nums, 0, (int)nums.size());
21 return res;
22 }
23};
非递归实现
可以通过反复调用 Next Permutation 实现。(参考资料(2))
子集
这题的朴素思路就是:
-
取出集合中的每个元素,求剩余元素的子集,各个推入结果列表
-
再把整体作为一个子集推入结果列表
代码:
1class Solution {
2 public:
3 void rec(vector<int> &nums, vector<int>& history, vector<vector<int>>& ret) {
4 if (nums.size() == 0) {
5 return;
6 }
7 // 注意推入的时机
8 ret.push_back(history);
9 // 下面都是常规的保存现场恢复现场
10 for (int i = 0; i < nums.size(); i++) {
11 int tmp = nums[i];
12 history.push_back(tmp);
13 nums.erase(nums.begin() + i);
14 rec(nums, history, ret);
15 nums.insert(nums.begin() + i, tmp);
16 history.pop_back();
17 }
18 }
19 vector<vector<int>> subsets(vector<int>& nums) {
20 vector<vector<int>> ret;
21 vector<int> history;
22 rec(nums, history, ret);
23 ret.push_back(nums);
24 return ret;
25 }
26};
输出:
1{
2 {}
3 {1}
4 {1, 2}
5 {1, 3}
6 {2}
7 {2, 1}
8 {2, 3}
9 {3}
10 {3, 1}
11 {3, 2}
12 {1, 2, 3}
13}
可以看到出现了重复。最简单的解决方法就是改用 set 结构。但是这样性能不佳。
无重复优化
发生重复的根源是什么?观察输出:
1{
2 {}
3 {1}
4 {1, 2}
5 {1, 3}
6 {2}
7 {2, 1} // 重复
8 {2, 3}
9 {3}
10 {3, 1} // 重复
11 {3, 2} // 重复
12 {1, 2, 3}
13}
注意到重复的原因在于回溯追加的元素小于首次选择的元素。比如 {2, 1} 中 $1 < 2$. 所以我们可以优化遍历时的起点:
1class Solution {
2 public:
3 void rec(vector<int> &nums, vector<int>& history, vector<vector<int>>& ret, int startIndex = 0) {
4 if (nums.size() == 0) {
5 return;
6 }
7 ret.push_back(history);
8
9 for (int i = startIndex; i < nums.size(); i++) { // 注意这里
10 int tmp = nums[i];
11 nums.erase(nums.begin() + i);
12 history.push_back(tmp);
13 rec(nums, history, ret, i);
14 history.pop_back();
15 nums.insert(nums.begin() + i, tmp);
16 }
17 }
18 vector<vector<int>> subsets(vector<int>& nums) {
19 vector<vector<int>> ret;
20 vector<int> history;
21 rec(nums, history, ret);
22 ret.push_back(nums);
23 return ret;
24 }
25};
通过引入 startIndex,直接跳过了重复项。
对比
对比全排列和子集的回溯穷举算法,可以发现在回溯途中推送解,就是子集的算法,在回溯的末端推送解,就是全排列的算法。
组合
我们从 1,2,3,4 中选 3 个,则相当于:
-
1+ 从2,3,4中选2个 -
2+ 从1,3,4中选2个 -
……
代码如下(已经进行了无重复优化):
1class Solution {
2 public:
3 void rec(vector<int>& nums, int k, vector<int>& history,
4 vector<vector<int>>& ret, int startIndex = 0) {
5 if (k == 0) {
6 ret.push_back(history);
7 return;
8 }
9 for (int i = startIndex; i < nums.size(); i++) {
10 int tmp = nums[i];
11 nums.erase(nums.begin() + i);
12 history.push_back(tmp);
13 rec(nums, k - 1, history, ret, i);
14 history.pop_back();
15 nums.insert(nums.begin() + i, tmp);
16 }
17 }
18 vector<vector<int>> combine(int n, int k) {
19 std::vector<int> nums(n);
20 for (int i = 0; i < n; i++) {
21 nums[i] = i + 1;
22 }
23 vector<vector<int>> ret;
24 vector<int> history;
25 rec(nums, k, history, ret);
26 return ret;
27 }
28};
性能很烂,怎么回事呢?
执行用时:76 ms, 在所有 C++ 提交中击败了7.87%的用户
内存消耗:8.8 MB, 在所有 C++ 提交中击败了96.70%的用户
剪枝优化
如果 n = 7, k = 4,从 5 开始搜索就已经没有意义了,这是因为:即使把 5 选上,后面的数只有 6 和 7,一共就 3 个候选数,凑不出 4 个数的组合。(参考)
根据上面这句话,假设终止条件是 $x$,则有 $n - x + 1 < k$,即 $x = n - k + 1$。
也就是说,如果 v[startIndex] > n - k + 1,则可以直接 return.
而 v[startIndex] = 1 + startIndex(因为题给条件说组合所用数为 $1\cdots n$)
所以 startIndex > n - k 可以直接退出。我们要限定 i <= n - k
1class Solution {
2 public:
3 void rec(vector<int>& nums, int k, vector<int>& history,
4 vector<vector<int>>& ret, int n, int startIndex = 0) {
5 if (k == 0) {
6 ret.push_back(history);
7 return;
8 }
9 for (int i = startIndex; i < nums.size() && i <= n - k; i++) {
10 int tmp = nums[i];
11 nums.erase(nums.begin() + i);
12 history.push_back(tmp);
13 rec(nums, k - 1, history, ret, n, i);
14 history.pop_back();
15 nums.insert(nums.begin() + i, tmp);
16 }
17 }
18 vector<vector<int>> combine(int n, int k) {
19 std::vector<int> nums(n);
20 for (int i = 0; i < n; i++) {
21 nums[i] = i + 1;
22 }
23 vector<vector<int>> ret;
24 vector<int> history;
25 rec(nums, k, history, ret, n, 0);
26 return ret;
27 }
28};
执行用时:60 ms, 在所有 C++ 提交中击败了8.58%的用户
内存消耗:8.7 MB, 在所有 C++ 提交中击败了97.13%的用户
空间优化
问题在哪儿?其实我们完全没必要维护一个 nums 数组,因为 nums 可以通过 i + 1 得出:
1class Solution {
2 public:
3 void rec(int k, vector<int>& history,
4 vector<vector<int>>& ret, int n, int startIndex = 0) {
5 if (k == 0) {
6 ret.push_back(history);
7 return;
8 }
9 for (int i = startIndex; i <= n - k; i++) {
10 history.push_back(i + 1);
11 rec(k - 1, history, ret, n, i + 1);
12 history.pop_back();
13 }
14 }
15 vector<vector<int>> combine(int n, int k) {
16 vector<vector<int>> ret;
17 vector<int> history;
18 rec(k, history, ret, n, 0);
19 return ret;
20 }
21};
执行用时:4 ms, 在所有 C++ 提交中击败了99.14%的用户
内存消耗:8.9 MB, 在所有 C++ 提交中击败了89.49%的用户
这样,节省了空间,也减少了操作步骤,使得计算速度提高了。
组合总和
给定一个无重复元素的正整数数组 candidates 和一个正整数 target ,找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。
candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同,则两种组合是唯一的。
对于给定的输入,保证和为 target 的唯一组合数少于 150 个。
示例 1:
输入: candidates = [2,3,6,7], target = 7
输出: [[7],[2,2,3]]
思路分析
分析:
如果采用排列穷举验证,相当于不剪枝,那么难点在于怎么处理重复元素。
不妨换个思路:可以利用 target - candidates[i] 缩小问题规模:
-
[2,3,6,7], target = 7-
-2, target = 5-
-2, target = 3 -
-3, target = 2 -
-6, target = -1 -
-7 target = -2
-
-
-3, target = 4 -
-6, target = 1 -
-7 target = 0
一旦 target = 0 就将搜索路径推送到答案列表。
一旦 target < 0 就停止搜索。
而可选数一直是
[2, 3, 6, 7] -
代码及无重复优化
参照这个例子写出代码,并进行无重复优化:
1class Solution {
2 private:
3 void backtrace(vector<int>& cand, vector<int>& path, vector<vector<int>>& ret,
4 int target, int startIndex = 0) {
5 if (target == 0) {
6 ret.push_back(path);
7 return;
8 }
9 if (target < 0) {
10 return;
11 }
12
13 for (int i = startIndex; i < cand.size(); i++) {
14 path.push_back(cand[i]);
15 backtrace(cand, path, ret, target - cand[i], i);
16 path.pop_back();
17 }
18 }
19
20 public:
21 vector<vector<int>> combinationSum(vector<int>& cand, int target) {
22 vector<vector<int>> ret;
23 vector<int> path;
24 backtrace(cand, path, ret, target);
25 return ret;
26 }
27};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:10.3 MB, 在所有 C++ 提交中击败了98.78%的用户
看起来不错。
N 皇后
N 皇后问题将回溯代入了二维世界(二次元)。但思路依旧是相同的 。
我们可以尝试各个初始位置,并锁定不能防止的单元:
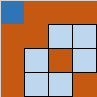
基本思路
斜向判断
基本代码
解法:
1#include <debug.h>
2
3class Solution {
4 private:
5 void printState(int n, map<int, bool> &history) {
6 cout << "state:" << endl;
7 for (int i = 0; i < n; i++) {
8 for (int j = 0; j < n; j++) {
9 cout << history[i * n + j] << " ";
10 }
11 cout << endl;
12 }
13 }
14 vector<string> historyToStrings(int n, map<int, bool> &history) {
15 vector<string> ret;
16 for (int i = 0; i < n; i++) {
17 string s(n, '.');
18 for (int j = 0; j < n; j++) {
19 if (history[i * n + j]) {
20 s[j] = 'Q';
21 }
22 }
23 ret.push_back(s);
24 }
25 return ret;
26 }
27 // 检查棋盘 i,j 位置是否允许落子
28 bool available(int n, int i, int j, map<int, bool> &history) {
29 // printState(n, history);
30 if (history[i * n + j]) {
31 return false;
32 }
33 // row,col 为当前检测的起点
34 for (int row = 0; row < n; row++) {
35 for (int col = 0; col < n; col++) {
36 // 一旦 row, col 处落子,则同行同列禁止落子
37 if (history[row * n + col]) {
38 if (row == i || col == j) {
39 return false;
40 }
41 // == 斜向检测,利用和/差为定值 ==
42 // p,q 为以 row,col 为起点的斜向元素的坐标
43
44 // 左斜向检测
45 auto coordSum = row + col;
46 // p 是临时 row
47 // q 是临时 col
48 // col = coordSum - row >= 0
49 int p = 0, q = coordSum - p;
50 while (q >= 0) {
51 if (p == i && q == j) {
52 return false;
53 }
54 p++;
55 q = (coordSum - p);
56 }
57
58 // 右斜向检测
59 // p q
60 auto coordDiff = row - col;
61 // col = row - coordDiff >= 0
62 p = 0, q = p - coordDiff;
63 while (p < n && q < n) {
64 if (p == i && q == j) {
65 return false;
66 }
67 p++;
68 q = p - coordDiff;
69 }
70 }
71 }
72 }
73 return true;
74 }
75 int placedCount(map<int, bool> &history) {
76 auto itr = history.begin();
77 int counter = 0;
78 while (itr != history.end()) {
79 if ((*itr).second) {
80 counter++;
81 }
82 itr++;
83 }
84 return counter;
85 }
86 void backtrace(int n, map<int, bool> &history, vector<vector<string>> &ret) {
87 if (placedCount(history) == n) {
88 auto state = historyToStrings(n, history);
89 // 重复则不添加
90 for (size_t i = 0; i < ret.size(); i++) {
91 if (state == ret[i]) {
92 return;
93 }
94 }
95 ret.push_back(state);
96
97 return;
98 }
99 bool anyAvaliable = false;
100 for (int i = 0; i < n; i++) {
101 string s(n, '.');
102 for (int j = 0; j < n; j++) {
103 if (available(n, i, j, history)) {
104 // printf("i,j = %d,%d placed \n", i, j);
105 anyAvaliable = true;
106 history[i * n + j] = true;
107 backtrace(n, history, ret);
108 history[i * n + j] = false;
109 }
110 }
111 }
112 if (!anyAvaliable) {
113 return;
114 }
115 }
116
117 public:
118 vector<vector<string>> solveNQueens(int n) {
119 // key: idx n*i+j, value: availability
120 map<int, bool> history;
121 for (int i = 0; i < n * n; i++) {
122 history[i] = false;
123 }
124
125 vector<vector<string>> ret;
126 backtrace(n, history, ret);
127 return ret;
128 }
129};
130int main(int argc, char const *argv[]) {
131 Solution s;
132 auto ret = s.solveNQueens(5);
133 print_vec_2d(ret, 0, true);
134 return 0;
135}
输出:
1.Q..,
2...Q,
3Q...,
4..Q.
5
6..Q.,
7Q...,
8...Q,
9.Q..
算法是对的,但是超时。
无重复优化
1
2class Solution {
3 private:
4 void printState(int n, map<int, bool> &history) {
5 cout << "state:" << endl;
6 for (int i = 0; i < n; i++) {
7 for (int j = 0; j < n; j++) {
8 cout << history[i * n + j] << " ";
9 }
10 cout << endl;
11 }
12 }
13 vector<string> historyToStrings(int n, map<int, bool> &history) {
14 vector<string> ret;
15 for (int i = 0; i < n; i++) {
16 string s(n, '.');
17 for (int j = 0; j < n; j++) {
18 if (history[i * n + j]) {
19 s[j] = 'Q';
20 }
21 }
22 ret.push_back(s);
23 }
24 return ret;
25 }
26 // 检查棋盘 i,j 位置是否允许落子
27 bool available(int n, int i, int j, map<int, bool> &history) {
28 // printState(n, history);
29 if (history[i * n + j]) {
30 return false;
31 }
32 // row,col 为当前检测的起点
33 for (int row = 0; row < n; row++) {
34 for (int col = 0; col < n; col++) {
35 // 一旦 row, col 处落子,则同行同列禁止落子
36 if (history[row * n + col]) {
37 if (row == i || col == j) {
38 return false;
39 }
40 // == 斜向检测,利用和/差为定值 ==
41 // p,q 为以 row,col 为起点的斜向元素的坐标
42
43 // 左斜向检测
44 auto coordSum = row + col;
45 // p 是临时 row
46 // q 是临时 col
47 // col = coordSum - row >= 0
48 int p = 0, q = coordSum - p;
49 while (q >= 0) {
50 if (p == i && q == j) {
51 return false;
52 }
53 p++;
54 q = (coordSum - p);
55 }
56
57 // 右斜向检测
58 // p q
59 auto coordDiff = row - col;
60 // col = row - coordDiff >= 0
61 p = 0, q = p - coordDiff;
62 while (p < n && q < n) {
63 if (p == i && q == j) {
64 return false;
65 }
66 p++;
67 q = p - coordDiff;
68 }
69 }
70 }
71 }
72 return true;
73 }
74 int placedCount(map<int, bool> &history) {
75 auto itr = history.begin();
76 int counter = 0;
77 while (itr != history.end()) {
78 if ((*itr).second) {
79 counter++;
80 }
81 itr++;
82 }
83 return counter;
84 }
85 void backtrace(int n, map<int, bool> &history, vector<vector<string>> &ret, int iStart = 0) {
86 if (placedCount(history) == n) {
87 auto state = historyToStrings(n, history);
88 ret.push_back(state);
89 return;
90 }
91 bool anyAvaliable = false;
92 for (int i = iStart; i < n; i++) {
93 string s(n, '.');
94 for (int j = 0; j < n; j++) {
95 if (available(n, i, j, history)) {
96 // printf("i,j = %d,%d placed \n", i, j);
97 anyAvaliable = true;
98 history[i * n + j] = true;
99 backtrace(n, history, ret, i + 1);
100 history[i * n + j] = false;
101 }
102 }
103 }
104 if (!anyAvaliable) {
105 return;
106 }
107 }
108
109 public:
110 vector<vector<string>> solveNQueens(int n) {
111 // key: idx n*i+j, value: availability
112 map<int, bool> history;
113 for (int i = 0; i < n * n; i++) {
114 history[i] = false;
115 }
116
117 vector<vector<string>> ret;
118 backtrace(n, history, ret);
119 return ret;
120 }
121};
搜索优化
上面的代码依然超时。原因在于我们判断可行区域时的效率太低。优化的方法是采用专门的结构,记录斜向是否可行。
1class Solution {
2 private:
3 vector<string> historyToStrings(int n, map<int, bool> &history) {
4 vector<string> ret;
5 for (int i = 0; i < n; i++) {
6 string s(n, '.');
7 for (int j = 0; j < n; j++) {
8 if (history[i * n + j]) {
9 s[j] = 'Q';
10 }
11 }
12 ret.push_back(s);
13 }
14 return ret;
15 }
16 void backtrace(int n, map<int, bool> &history, vector<bool> &curRow,
17 vector<bool> &diag1, vector<bool> &diag2,
18 vector<vector<string>> &ret, int iStart = 0) {
19 if (placedCount(history) == n) {
20 auto state = historyToStrings(n, history);
21 ret.push_back(state);
22 return;
23 }
24 bool anyAvaliable = false;
25 for (int i = iStart; i < n; i++) {
26 for (int j = 0; j < n; j++) {
27 if (curRow[j] || diag1[j + i] || diag2[j + n - 1 - i]) {
28 continue;
29 }
30 // printf("i,j = %d,%d placed \n", i, j);
31 anyAvaliable = true;
32
33 history[i * n + j] = true;
34 curRow[j] = diag1[j + i] = diag2[j + n - 1 - i] = true;
35 backtrace(n, history, curRow, diag1, diag2, ret, i + 1);
36 history[i * n + j] = false;
37 curRow[j] = diag1[j + i] = diag2[j + n - 1 - i] = false;
38 }
39 }
40 if (!anyAvaliable) {
41 return;
42 }
43 }
44
45 public:
46 vector<vector<string>> solveNQueens(int n) {
47 // key: idx n*i+j, value: availability
48 map<int, bool> history;
49 for (int i = 0; i < n * n; i++) {
50 history[i] = false;
51 }
52 vector<bool> curRow(n);
53 vector<bool> diag1(2 * n - 1);
54 vector<bool> diag2(2 * n - 1);
55 vector<vector<string>> ret;
56 backtrace(n, history, curRow, diag1, diag2, ret);
57 return ret;
58 }
59};
执行用时:636 ms, 在所有 C++ 提交中击败了5.15%的用户
内存消耗:7.8 MB, 在所有 C++ 提交中击败了32.43%的用户
无效解优化
我们的代码还有优化空间,如果棋盘第一行(或者列)没有放置过,它还会尝试第二行。但既然已经有一行(或者列)没有放置过,那么必然无法放满 N 个。可以通过一个标识来跳过这种情况:
1
2class Solution {
3 private:
4 vector<string> historyToStrings(int n, map<int, bool> &history) {
5 vector<string> ret;
6 for (int i = 0; i < n; i++) {
7 string s(n, '.');
8 for (int j = 0; j < n; j++) {
9 if (history[i * n + j]) {
10 s[j] = 'Q';
11 }
12 }
13 ret.push_back(s);
14 }
15 return ret;
16 }
17 void backtrace(int n, map<int, bool> &history, vector<bool> &curRow,
18 vector<bool> &diag1, vector<bool> &diag2,
19 vector<vector<string>> &ret, int iStart = 0) {
20 if (iStart == n) {
21 auto state = historyToStrings(n, history);
22 ret.push_back(state);
23 return;
24 }
25 bool rowPlaced = false;
26 for (int i = iStart; i < n; i++) {
27 for (int j = 0; j < n; j++) {
28 if (curRow[j] || diag1[j + i] || diag2[j + n - 1 - i]) {
29 continue;
30 }
31 // printf("i,j = %d,%d placed \n", i, j);
32 rowPlaced = true;
33 history[i * n + j] = true;
34 curRow[j] = diag1[j + i] = diag2[j + n - 1 - i] = true;
35 backtrace(n, history, curRow, diag1, diag2, ret, i + 1);
36
37 rowPlaced = false;
38 history[i * n + j] = false;
39 curRow[j] = diag1[j + i] = diag2[j + n - 1 - i] = false;
40 }
41 if (!rowPlaced) {
42 return;
43 }
44 }
45
46 return;
47 }
48
49 public:
50 vector<vector<string>> solveNQueens(int n) {
51 // key: idx n*i+j, value: availability
52 map<int, bool> history;
53 for (int i = 0; i < n * n; i++) {
54 history[i] = false;
55 }
56 vector<bool> curRow(n);
57 vector<bool> diag1(2 * n - 1);
58 vector<bool> diag2(2 * n - 1);
59 vector<vector<string>> ret;
60 backtrace(n, history, curRow, diag1, diag2, ret);
61 return ret;
62 }
63};
执行用时:8 ms, 在所有 C++ 提交中击败了57.32%的用户
内存消耗:7.8 MB, 在所有 C++ 提交中击败了31.88%的用户
这次执行时间足足提高了上百倍。
返回值优化
由于我们上面为了代码的结构性,流水式处理,history 状态和状态的展现采用的是不同的方式,后者通过前者经过 historyToStrings 函数转换。这样会增加调用次数。
下面我们采用 history 直接作为返回状态:
1
2class Solution {
3 private:
4 void backtrace(int n, vector<string> &history, vector<bool> &curRow,
5 vector<bool> &diag1, vector<bool> &diag2,
6 vector<vector<string>> &ret, int iStart = 0) {
7 if (iStart == n) {
8 ret.push_back(history);
9 return;
10 }
11 bool rowPlaced = false;
12 for (int i = iStart; i < n; i++) {
13 for (int j = 0; j < n; j++) {
14 if (curRow[j] || diag1[j + i] || diag2[j + n - 1 - i]) {
15 continue;
16 }
17 // printf("i,j = %d,%d placed \n", i, j);
18 rowPlaced = true;
19 history[i][j] = 'Q';
20 curRow[j] = diag1[j + i] = diag2[j + n - 1 - i] = true;
21 backtrace(n, history, curRow, diag1, diag2, ret, i + 1);
22
23 rowPlaced = false;
24 history[i][j] = '.';
25 curRow[j] = diag1[j + i] = diag2[j + n - 1 - i] = false;
26 }
27 if (!rowPlaced) {
28 return;
29 }
30 }
31 }
32
33 public:
34 vector<vector<string>> solveNQueens(int n) {
35 // key: idx n*i+j, value: availability
36 vector<string> history(n);
37 for (int i = 0; i < n; i++) {
38 history[i] = string(n, '.');
39 }
40 vector<bool> curRow(n);
41 vector<bool> diag1(2 * n - 1);
42 vector<bool> diag2(2 * n - 1);
43 vector<vector<string>> ret;
44 backtrace(n, history, curRow, diag1, diag2, ret);
45 return ret;
46 }
47};
执行用时:4 ms, 在所有 C++ 提交中击败了95.27%的用户
内存消耗:7 MB, 在所有 C++ 提交中击败了90.23%的用户
执行时间降低了已经比较令人满意了。
回溯实现深度优先搜索
给定一棵树,要求搜索某个节点,并返回其路径。参考代码:
1 void FindPathImpl(stack<TreeNode *> &history, TreeNode *root,
2 TreeNode *target, bool &over) {
3 if (over) {
4 return;
5 }
6 history.push(root);
7 if (root == nullptr) {
8 return;
9 }
10 if (root == target) {
11 over = true;
12 return;
13 }
14 FindPathImpl(history, root->left, target, over);
15 if (over) {
16 return;
17 } else {
18
19 history.pop();
20 }
21 FindPathImpl(history, root->right, target, over);
22 if (over) {
23 return;
24 } else {
25
26 history.pop();
27 }
28 }
29 deque<TreeNode *> FindPath(TreeNode *root, TreeNode *target) {
30 stack<TreeNode *> history;
31 bool found = false;
32 FindPathImpl(history, root, target, found);
33 // reverse
34 deque<TreeNode *> ret;
35 while (!history.empty()) {
36 auto top = history.top();
37 history.pop();
38 ret.push_back(top);
39 }
40 return ret;
41 }
参考
(1)【算法】回溯法四步走 - Nemo& - 博客园 (cnblogs.com):比较通俗易懂,推荐。
(2)Next lexicographical permutation algorithm (nayuki.io):“下一个全排列”算法,很厉害。
(3)回溯算法入门级详解 + 练习(持续更新) - 全排列 - 力扣(LeetCode) (leetcode-cn.com)
