红黑树为什么这样红——从 AVL 到 RBT
红黑树(下文简称 rbt)曾经是最让我懵逼的数据结构。看了无数教材、文章、视频,始终不能理解为啥要这么设计。后来学 XFS 文件系统时搞懂 B+tree 之后,才有了更深的理解。
BST(二叉搜索树)比较简单就略过。
bf 是 平衡因子 的简写。
AVL 树
AVL 是最先被提出的自平衡二叉查找树,说它平衡是因为满足 $|h(ls) - h(rs)| \leq 1$ 。
Node 保存如下状态:key, value, height。之所以保存 height 是因为需要计算平衡因子从而重平衡。
平衡因子:左右子树高度差
bf = left.height - right.height。高度:不同人的定义不同,但本质就是用来比较偏序关系。在本文中,下面这棵树的高度为 3.
平衡因子和旋转方式
平衡因子的重要意义在于判断“扭”的方向,从而选择对应的旋转方式。旋转一度是让人头疼的环节,实际上我有办法让你不用记。来看看吧。
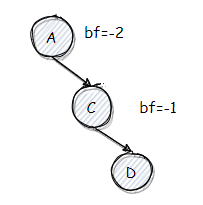
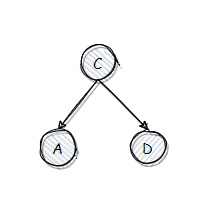
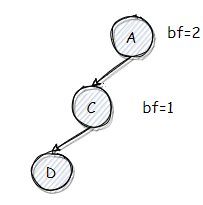
cur.bf < 0 && cur.right.bf < 0,明显太靠右了(俗称 RR 型),需要采用左旋。由于二叉树性质可知 A < C < D,因此旋转后必然是 C 在中间,A、D 分列左右:
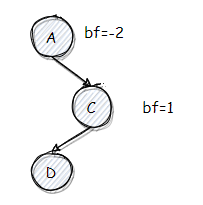
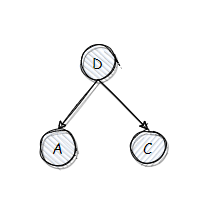
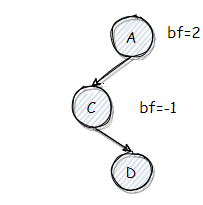
cur.bf < 0 && cur.right.bf > 0,俗称 RL 型,由于二叉树性质可知 A < D < C,因此旋转后必然是 D 在中间,A,C 分列左右:
对于 LL 和 LR 的情况,是类似的,很简单,就不细说了。
插入
按常规 BST 方式,递归插入,并沿递归路径更新 height(取左右者更高者+1),对不平衡的结点进行重平衡。
重平衡的流程如下:
-
若
bf > 1,说明左子树偏高,根据子树 bf,选择平衡策略。 -
若
bf < 1,说明右子树偏高,根据子树 bf,选择平衡策略。
删除
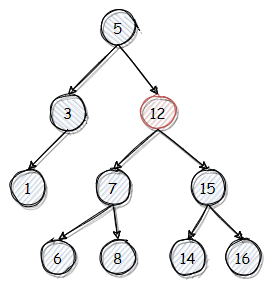
我们从下面这棵树删除 12,此步骤分为两步:先找到 12,再找到 12 的继承结点,取代 12,然后重平衡。而继承结点是指至少有一个空子树的子结点。下图中,以 8 作为继承结点,取代 12。由于取代后平衡,所以没有重平衡的步骤。
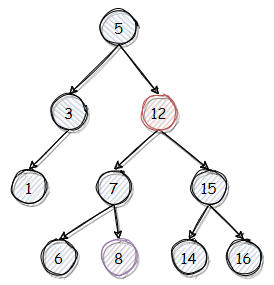
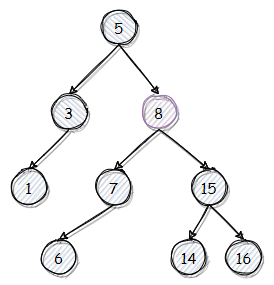
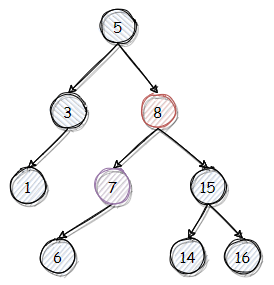
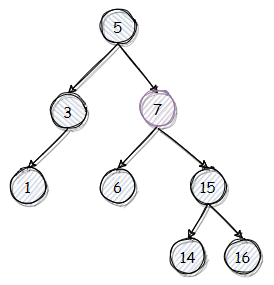
我们再以继续删除 8 为例。由于 7 没有右子树,可以作为继承结点。因此将 7 取代 8 即可。
B-Tree 之 2-3 树
2-3 树是 B-树的最小形式。2-3 树的意思是,每个结点内最多存 2 个值,最多有 3 个子结点。
插入
B-tree 插入的特别之处在于需要分裂。具体来说,插入规则如下:
-
搜索 B 树以找到可以插入该结点的相应叶结点。
-
如果叶结点包含的 Key 少于 m-1,则按递增顺序插入元素。
-
否则,如果叶结点包含 m-1 个 Key,按照以下步骤操作。
-
-
按元素的递增顺序插入新元素。
-
将结点拆分为中位数处的两个结点。
-
将中位数元素向上推送到其父结点。
-
如果父结点还包含 m-1 个键,则按照相同的步骤将其拆分。
-
其中:m 是子结点数量上限。对于 2-3 树,m = 3
下面,通过例子领悟插入的方法。
例子:将 5、3、12、1、7、15、6、8、14、16 插入 2-3 树。
(1)【5 的插入】创建根结点 5
(2)【3 的插入】由于 3 < 5,且根结点有空,所以就地插入 3.

(3)【12 的插入】由于 12 大于 5,插入到 5 右边。注意到满了。
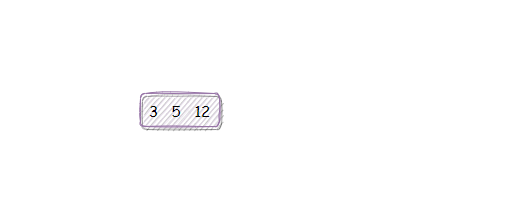
满了,所以将结点拆分为中位数处的两个结点:3、12。将中位数元素 12 向上推送到其父结点。
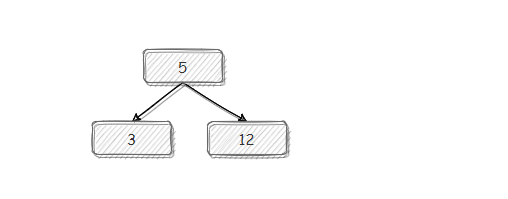
达到稳定状态,插入完成。
(4)【1 的插入】由于 1 < 5,所以选择左边分支。由于 1 < 3 所以在 3 的左边插入。稳定。
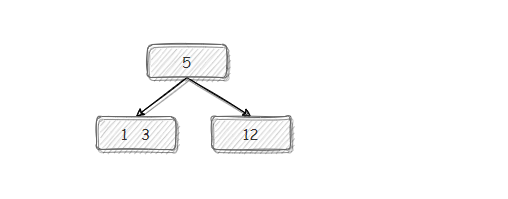
(5)【7 的插入】不赘述,简单插入后,稳定。
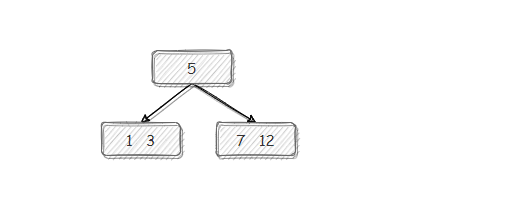
(6)【15 的插入】简单插入后,满。
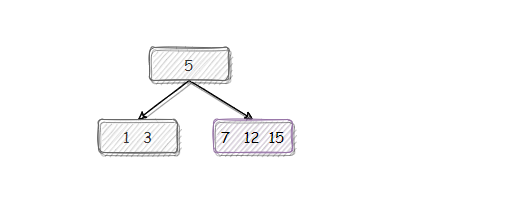
所以从 12 拆分
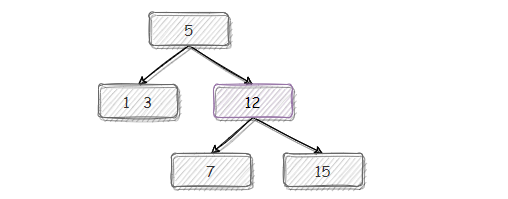
12 上提
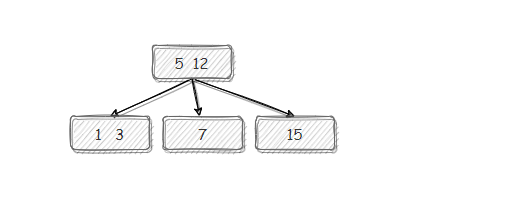
然后稳定了。
(7)【6 的插入】简单插入。
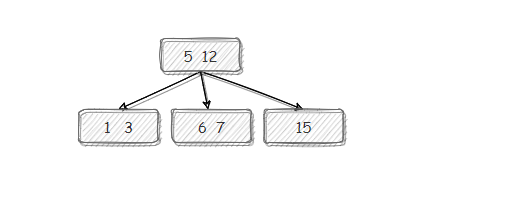
(8)【8 的插入】简单插入后满。需要分裂。
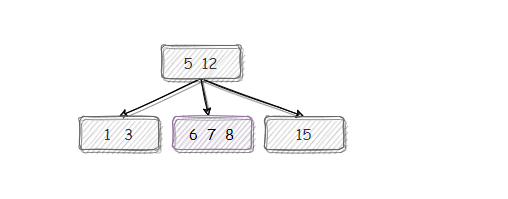
分裂:
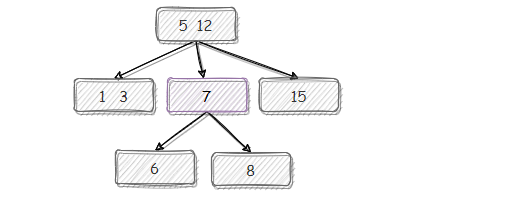
上提:
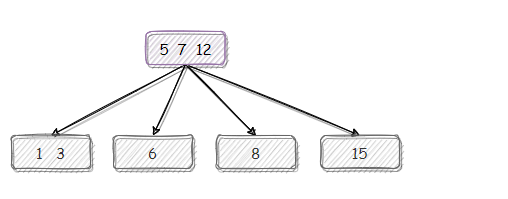
上提后父结点不稳定,继续分裂:
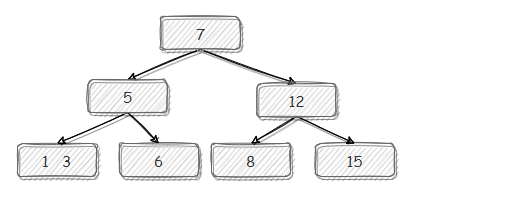
此时稳定。
(9)【14 的插入】简单插入。
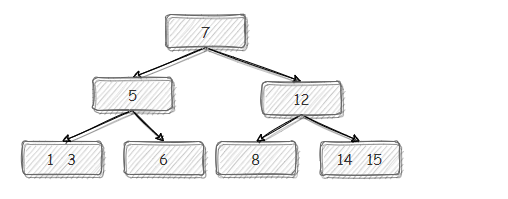
(10)【16 的插入】简单插入,满,需要分裂。
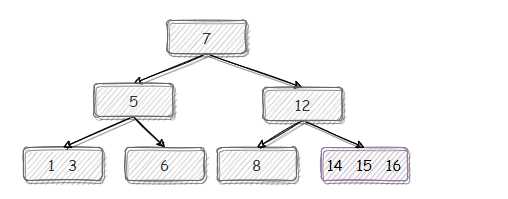
分裂:
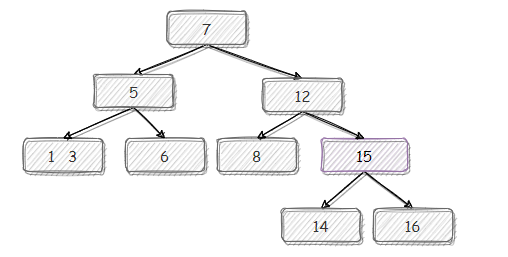
最后上提:
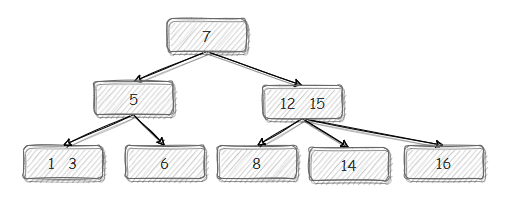
完成所有插入操作。
删除
删除的结点可以是叶结点,也可以是内部结点。
叶结点删除的步骤如下:
-
找到叶结点。
-
如果叶结点中的键数超过 m/2(下取整,对于我们的情况是 1),则从结点中删除所需的键。
-
如果叶结点不超过 m/2 键,则通过从左或右同级元素中获取元素来完成键。
-
-
如果左同级元素包含的 m/2 个以上元素,则将其最大元素向上推到其父元素,并将中间元素向下移动到删除键的结点。
-
如果右同级元素包含的 m/2 个以上元素,则将其最小元素向上推送到父元素,并将中间元素向下移动到删除键的结点。
-
-
如果两个同级结点都包含的 m/2 个元素都不超过 m/2 个,则通过连接两个叶结点和父结点的中间元素来创建新的叶结点。
-
如果父结点少于 m/2 个,则也对父结点应用上述过程。
若删除内部结点,则将该结点替换为其顺序的后续结点或前置结点。由于后续结点或前置任务将始终位于叶结点上,因此,当从叶结点中删除结点时,该过程将类似。
我们继续上面的图,从中依次删除 7、3、15

(1)【7 的删除】由于 7 是内部结点,所以首先找到 7 的前置结点。即比 7 小的最大的结点。是 6.

用 6 代替 7

然后处理原来这个 6 (叶子)的删除。由于删除后就没了,少于 m/2 个,所以需要从左同级结点分一些过来。由于左同级结点 1 3 两个,大于 m/2 个,所以 3 上推到 5 所在结点,中间结点 5 下移到 6 原来的位置(类似右旋)

(2)【3 的删除】用 1 代替。

然后处理原 1 的删除。

右边同级元素(Node 5)不超过 m/2=1 个,所以 5 上移。

(3)【15 的删除】用 14 取代。

取代后,发现原位置左同级元素不超过 1 个,而上方结点 (Node 12 14) 有俩,所以中间元素 12 下沉与 8 合并。


补充:如何寻找 BST/B-tree 的前结点
上面说“首先找到 7 的前置结点”,但没说算法如何实现。下面举个例子。

如何找到 6 的前置结点?首先,选取左孩子 3 为起点,然后往它右边一把梭。我们看到了 4,4 的右边是 5. 所以答案是 5.
如何找到 6 的后置结点?首先,选取右孩子 12 为起点,然后往它左边一把梭。我们看到了 7,7 左边没了。所以答案是 7.
拆分
左倾红黑树
从红色链接 2-3 树推出红黑树
2-3 树有一个缺点——不是二叉树。那么,有没有办法对其进行等价变换,从而可以既有 2-3 树的廉价平衡性,又像二叉树那样节省空间呢?
显然,2-3 树的结点只有两种状态:一个元素,或两个元素。因此对一个 2-3 树结点,只要 1~2 个二叉树结点就能表示。
一种朴素的映射规则如下:

用此规则转换一棵 2-3 树看看:
我们按照 1 2 3 4 5 6 7 8 9 10 的顺序构建一棵 2-3 树。

你会发现,诶,竟然可以完美的对应。而右边,居然得到了一棵红黑树。什么,没看出来?我们换个颜色看看:

你可以对照红黑树的性质,发现完全满足:
-
结点是红色或黑色。
- 因为红色表示这是一个 2-3 树的 2 元素结点的最左元素。
-
根是黑色。
- 因为根结点不可能是最左元素。
-
所有叶子都是黑色(叶子是NIL结点)。
- 算上 NIL 结点(即数据结点下面的隐藏结点),同样满足。
-
不存在两个相邻的红色结点,相邻指两个结点是父子关系。
- 这是 2-3 树结点的 2 元素结点的最左元素,其右边必然有另一个元素,转换到红黑树就是最左元素的父元素。
-
从任一结点到其每个叶子的所有简单路径都包含相同数目的黑色结点。
- 这是显然的,因为红色结点在 2-3 树中与其父结点同级
左倾红黑树并不完美
左倾红黑树虽然易于实现,但是并不能涵盖各种类型的红黑树。它的红结点基于向左的链接标记而来,但红黑树可以是各种形态。例如:

但是,对于理解记忆性质而言,2-3 树同构而来的左倾红黑树,无疑是非常有用的。
倾红黑树不止一种
2-3 树,2-3-4 树分别都有对应的左倾红黑树和右倾红黑树,组合起来有四种。
传统红黑树
旋转
旋转是易于理解的。旋转的核心就在于逆转支配关系。
左旋:
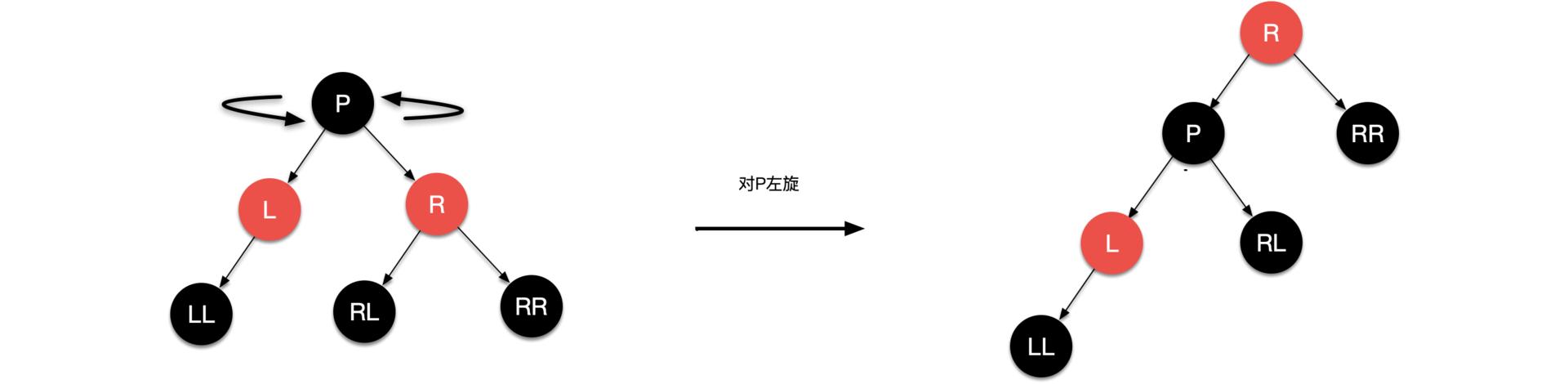
右旋
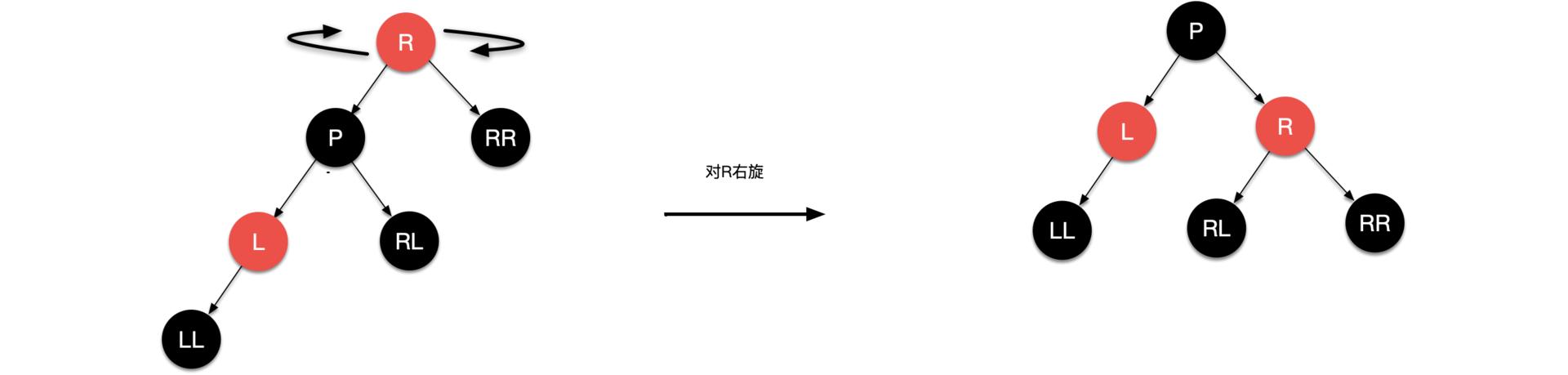
插入
插入时,将正插入结点的颜色设置为默认红色。分五种情况讨论
(1)插入空树:直接变黑。
(2)插入结点 Key 已存在:在对应位置替换,使用对应颜色。
(3)插入结点的父结点是黑色结点:直接插入
(4)插入到红底三角:两层反色。并将 PP 结点当作插入结点,处理更上层的情况。
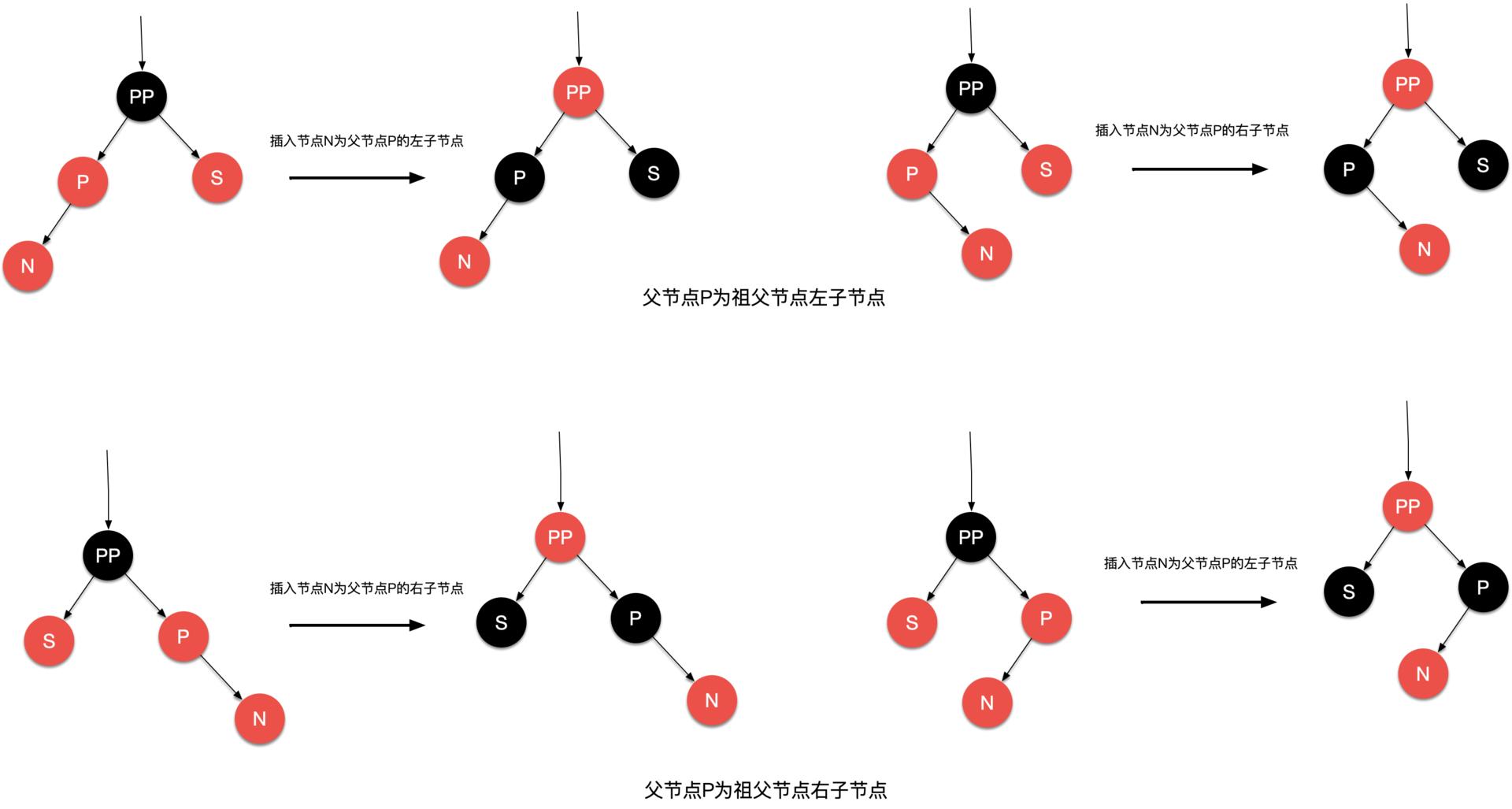
(5)
-
左插入到双色底三角中的红方
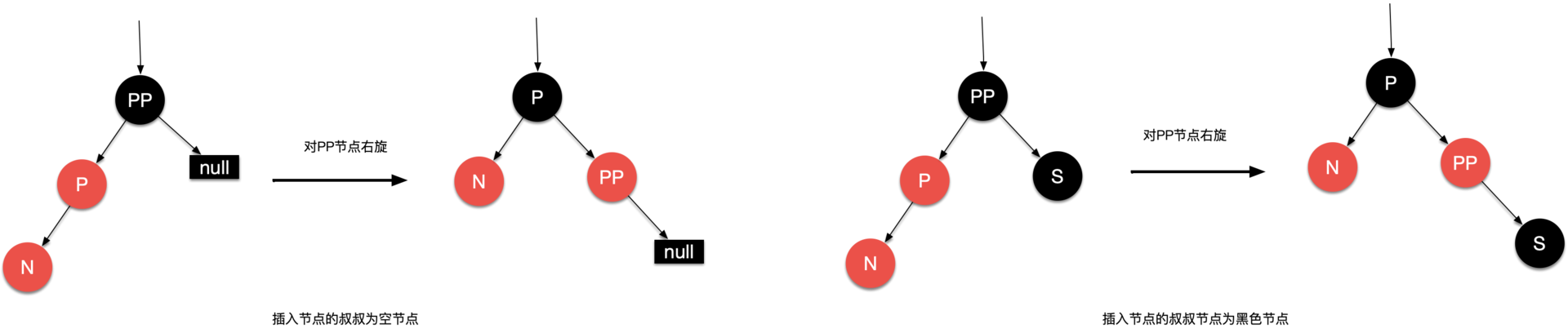
-
右插入到双色底三角中的红方
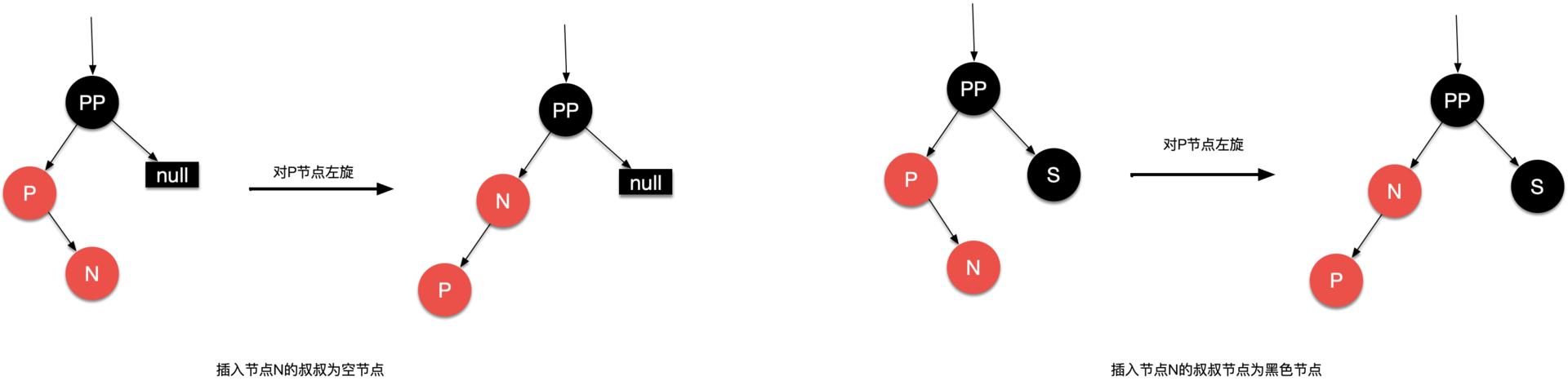
-
- 上述情况的对称情况
替换
删除结点之后,可以找到两个替换结点,即可以用左子树中的最大值以及右子树中的最小值来替换删除结点。
根据被删结点的子结点数:
-
情景1:删除结点无子结点,可以直接删除,无需替换
-
情景2:删除结点只有一个子结点,用子结点替换删除结点
-
情景3:删除结点有两个子结点,可以用后继结点或者前继结点替换删除结点。本文采用前者,即后继结点替换删除结点
删除
删除结点可等同于删除替换结点
通俗易懂的红黑树图解(上) - 政采云前端团队 (zoo.team)
通俗易懂的红黑树图解(下) - 政采云前端团队 (zoo.team)

