用隐马尔可夫模型预测股票(大雾)
2019211379 张梓靖
隐马尔可夫模型(HMM)
基本概念
先从基本概念讲起。
马尔可夫性质:当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态;换句话说,在给定现在状态时,它与过去状态(即该过程的历史路径)是条件独立的,那么此随机过程即具有马尔可夫性质。
我的理解:一个状态机的次态,如果只取决于现态,而非依赖历史状态,则此状态机是隐马尔可夫性质的。
马尔可夫过程:是一个具备了马尔可夫性质的随机过程。
我的理解:是一个状态转移链,其中对于每个状态,只依赖于上一个状态
隐性马尔可夫模型:用来描述一个含有隐含未知参数的马尔可夫过程(维基百科)。感觉没说清楚,另一种说法:是一个概率模型,用来描述一个系统隐性状态的转移和隐性状态的表现概率。
请移步:如何用简单易懂的例子解释隐马尔可夫模型? - 知乎 (zhihu.com)
总结
-
我们无法观察到基因型(内在状态),但是可以观察出表现型(隐性状态产生的外在表现)。
-
我们连续观测一串表现型(称为 可见状态链),其对应一串基因型(隐含状态链)
-
在某隐含状态,表现出某可见状态的概率,称为输出概率
建模
一个 HMM 可以以一个如下的三元组表示:
1 def __init__(self, trans_pbb: np.ndarray, emit_pbb: np.ndarray, init_pbb: np.ndarray):
2 """初始化隐马尔可夫模型
3
4 Args:
5 trans_pbb (np.ndarray): 转移概率矩阵
6 emit_pbb (np.ndarray): 输出概率矩阵
7 init_pbb (np.ndarray): 初始概率分布
8 """
9 self.trans_pbb = trans_pbb
10 self.emit_pbb = emit_pbb
11 self.init_pbb = init_pbb
12 self.n_states = len(init_pbb)
数学记号约定
-
$Z$:隐状态。内部的各个状态。个数为 $m$。
-
第 $k$ 个状态,记作 $z_k$。
-
某个状态下的概率分布,记作 $P(x_k|x)$。
-
-
$X$:输出的观测数据。$n$ 种取值,序列长度为 $l$。
-
第 $k$ 个观测数据,记作 $x_k$
-
第 $[k, n]$ 个观测序列,记作 $x_{k:n}$
-
-
$A$:$m \times m $ 状态转移矩阵。下一刻,从_某状态_ 转移到_某状态_ 的概率。
-
$B$:$m \times n $ 发射概率矩阵。状态 生成 输出 的概率。
-
$\pi$ :$m\times 1$初始状态概率矩阵。初始情况处于 状态 的概率。
题目
假设状态数 $\left| Q \right| = 3$ ,分别代表:牛市、熊市、稳定市场。状态到观测的发射模型是一个多项式分布。假设输出的观测个数 $\left| O \right| = 5$ ,分别对应的含义如下表。
| output symbol | description | % daily change |
|---|---|---|
| 1 | large drop | $< -2\%$ |
| 2 | small drop | $-2\% < x < -1\%$ |
| 3 | no change | $-1\% < x < 1\%$ |
| 4 | small rise | $1\% < x < 2\%$ |
| 5 | large rise | $> 2\%$ |
考虑序列长度 $T = 100$ ,对应于 $100$ 个连续的交易日。假设 $HMM$ 的模型参数已知(已经通过 EM 算法在一个较大的数据集上完成了参数的估计),数据来源于 Yahoo!金融。在 hmm_params.dat 文件中,可以看到下面的参数:
-
$\text{transition}$ : 状态转移矩阵,$\operatorname{transition}(i,j) = P(q_{t+1} = j | q_t = i)$
-
$\text{emission}$ : 发射概率矩阵,$\operatorname{emission}(i,j) = P(o_t = j | q_t = i)$
-
$\text{prior}$ : 初始状态概率向量,$\operatorname{prior}(i) = P(q_0 = i)$
-
$\text{price\_change}$ : 观测序列,$\operatorname{price\_change}(i) = \frac{ \operatorname{price}(i) - \operatorname{price}(i-1) }{ \operatorname{price}(i-1) }$
本题目的任务是根据模型参数,完成 100 个交易日上的推断,并预测接下来的 28 天的观测值:
(1)根据时间序列 $t= 1, 2, \ldots, 100$ ,上的观测,使用 Forward-Backward 算法,推断其背后的隐状态,即计算 $P(q_t = i | o_1, o_2, \ldots, o_{100})$,并绘制 $t = 1, 2, \ldots, 100$ 上三个不同状态对应的状态序列。
(2)采用 Viterbi 算法,推断时间序列 $t = 1, 2, \ldots, 100$ 上最可能的状态序列 $q_1, q_2, \ldots, q_100$.
(3)推断时刻 $t = 101, 102, \cdots , 128$ 上的输出。
即预测 t=100 之后的 28 个观测值
使用 Forward 算法估计 $P(q_{t-1} | o_{t-101}, o_{t-100}, \ldots, o_{t-1})$,其中 $o_{t-101}, o_{t-100}, \ldots, o_{t-1}$ 为已知输出。
通过状态转移矩阵,从 $P(q_{t-1})$ 计算 $P(q_t)$ 。从 $P(q_t)$ 中抽样一个 $\hat{q_t}$ ,从 $P(o_t| \hat{q_t}) $ 中抽样得到一个 $\hat{o}_t$ ,与 $t =101, \cdots , 128$ 上的标准输出做对比,计算模型预测的准确率。重复一百次,计算预测结果的均值和方差。
我的答案
约定:
牛市、熊市、稳定市场分别用 0,1,2 表示。
观测值统一从 0 开始计算,即用 0,1,2,3,4 表示。
(1)状态转换图如下:
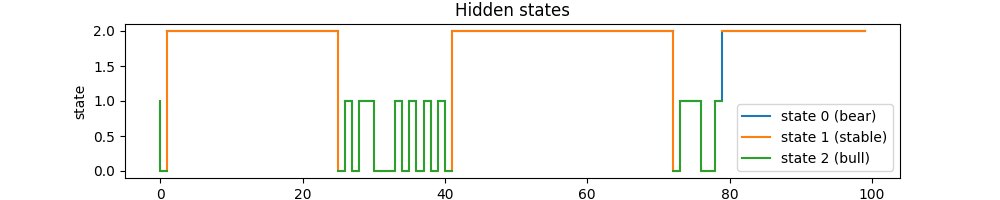
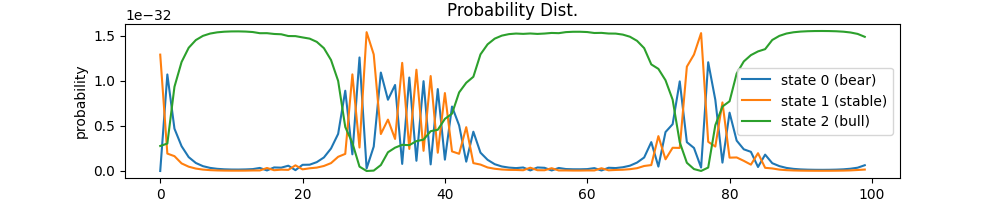
利用概率分布为 gamma = alpha * beta 这一性质,求得各个状态的 gamma 概率分布图如下:
计算结果如下:
alpha=
[[1.10477954e-29 4.20081524e-02 1.53906122e-02 7.53517792e-03
3.51507416e-03 1.69940551e-03 8.51403213e-04 4.51964878e-04
2.59117947e-04 1.62388608e-04 1.10984664e-04 8.14712284e-05
// 中略
1.40306780e-22 1.17341134e-22 9.55478687e-24 7.97282230e-24
6.69365473e-24 5.60613765e-24 2.89245215e-25 2.35643217e-26
4.71407924e-32 3.08244389e-30 3.42312071e-29 3.91656529e-30
3.54466819e-30 4.15081494e-30 3.91246939e-30 3.48283780e-30
1.85420998e-31 1.57980638e-31 1.42037694e-31 1.22496219e-31
1.04208779e-31 8.79432478e-32 7.39053073e-32 6.19666289e-32
5.18922383e-32 4.34264188e-32 3.63283658e-32 3.03843878e-32
2.54101652e-32 2.12489985e-32 1.77686825e-32 1.48581324e-32]]
beta=
[[2.12738150e-31 2.54495858e-31 3.04528536e-31 3.64569112e-31
4.36822832e-31 5.24217660e-31 6.30891388e-31 7.63184728e-31
9.31729158e-31 1.15589675e-30 1.47357788e-30 1.96070594e-30
2.79205484e-30 4.18126827e-30 8.28733945e-30 4.68425065e-29
7.15579048e-29 1.15212249e-28 2.48857800e-28 1.32576020e-27
2.25719385e-27 4.16921077e-27 8.20602764e-27 1.68277324e-26
3.58284927e-26 7.34886039e-26 1.94364669e-25 8.52129443e-25
// 中略
2.17784576e-03 2.60026277e-03 3.10082214e-03 3.68421946e-03
7.14224825e-02 8.54148824e-02 1.02148195e-01 1.22158919e-01
1.46088082e-01 1.74701029e-01 2.08910275e-01 2.49801029e-01
2.98657818e-01 3.56987718e-01 4.26529387e-01 5.09222525e-01
6.07083618e-01 7.21836578e-01 8.54291398e-01 1.00000000e+00]]
gamma=
[[2.35028756e-60 1.06909008e-32 4.68688059e-33 2.74709312e-33
// 中略
4.44059367e-34 1.81176681e-33 8.65364353e-34 5.40101215e-34
3.40852102e-34 2.34809429e-34 1.77261351e-34 1.47083858e-34
1.32852892e-34 1.29217590e-34 1.34807083e-34 1.51737233e-34
1.86284755e-34 2.52311185e-34 3.67171922e-34 6.40224472e-34]
[1.28861097e-32 1.92741212e-33 1.64271988e-33 8.41332168e-34
// 中略
2.67748108e-35 2.57346040e-35 2.77276837e-35 3.34984316e-35
4.52706081e-35 6.70348258e-35 1.10845807e-34 1.59293530e-34]
[2.77154071e-33 3.03933747e-33 9.32804988e-33 1.20692251e-32
1.36455173e-32 1.44976014e-32 1.49635868e-32 1.52169658e-32
// 中略
1.52236607e-32 1.53637759e-32 1.54395780e-32 1.54793277e-32
1.54980227e-32 1.55026982e-32 1.54951156e-32 1.54724147e-32
1.54260950e-32 1.53383044e-32 1.51796326e-32 1.48581324e-32]]
gamma=
[1 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 1 0 1 1 0 0 0 1 0 1
0 1 0 1 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0
1 1 1 0 0 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
(2)状态转换图如下:

Viterbi 路径如下(注:从 0 开始计算,即实际使用时,值要**+1**):
viterbi_seq=
[2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 1 1 1 0 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 1 1 0 1 0
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2]
(3)先看第一种计算机方式。只看输出值的准确率。
1 n_seq = 28 # 预测长度
2 n_turn = 100 # 随机次数
3
4 # == 使用前向算法,估计最后一个状态的概率分布 ==
5 # 由于已经在前面调用过,所以我们直接使用 alpha 计算结果
6 alpha_last = alpha[:, 99]
7 output_real = ob_seq[100:128] # 实际值
8
9 # 最后状态。根据前向算法得出
10 forward_last_state = np.argmax(alpha_last)
11 price_seq_real = _reduce_output(output_real) # 真实价格序列
12 acc_seq = np.zeros(n_turn)
13 # 进行 n_turn 次模拟
14 for turn in range(n_turn):
15 last_state = forward_last_state
16 output_fit = np.zeros(n_seq) # 预测值
17 for t in range(n_seq):
18 # 按照状态转移概率分布,抽取一个状态
19 state = np.random.choice(
20 np.arange(3), p=model.trans_pbb[last_state])
21 # 按照此状态到各个观测值的概率,抽取一个观测值
22 output = np.random.choice(np.arange(5), p=model.emit_pbb[state, :])
23 output_fit[t] = output
24
25 last_state = state
26 from sklearn.metrics import precision_score
27 acc_seq[turn] = precision_score(output_real, output_fit, average='micro')
28
29
30 # 输出拟合度的均值和标准方差
31 print("acc_seq=")
32 print(acc_seq)
33 print("acc_seq.mean=")
34 print(acc_seq.mean())
35 print("acc_seq.std=")
36 print(acc_seq.std())
结果:
acc_seq=
[0.67857143 0.64285714 0.75 0.71428571 0.75 0.71428571
0.71428571 0.60714286 0.78571429 0.42857143 0.75 0.75
0.64285714 0.71428571 0.46428571 0.67857143 0.78571429 0.67857143
0.67857143 0.67857143 0.60714286 0.39285714 0.60714286 0.60714286
0.35714286 0.78571429 0.57142857 0.67857143 0.60714286 0.67857143
0.78571429 0.75 0.67857143 0.78571429 0.82142857 0.60714286
0.71428571 0.85714286 0.64285714 0.67857143 0.67857143 0.64285714
0.75 0.64285714 0.67857143 0.64285714 0.60714286 0.67857143
0.75 0.60714286 0.57142857 0.75 0.82142857 0.71428571
0.57142857 0.64285714 0.60714286 0.67857143 0.75 0.64285714
0.57142857 0.82142857 0.67857143 0.60714286 0.64285714 0.60714286
0.60714286 0.71428571 0.75 0.53571429 0.57142857 0.67857143
0.53571429 0.75 0.71428571 0.78571429 0.64285714 0.75
0.71428571 0.67857143 0.57142857 0.75 0.75 0.78571429
0.67857143 0.78571429 0.67857143 0.75 0.67857143 0.75
0.42857143 0.60714286 0.71428571 0.71428571 0.53571429 0.60714286
0.60714286 0.53571429 0.67857143 0.78571429]
acc_seq.mean=
0.6700000000000002
acc_seq.std=
0.09383006784956015
这种方式计算出来准确率有 65~70%. 方差只有 0.09.
然而……
(4)显然这不能无法用于指导投资股票。问题在于:上面只计算了序列模型拟合出某个输出的精确率。但如果考虑到股市的涨跌的累积效应,我们可以以 t=101 作为 1,设置观测值与涨跌百分比的映射,进行累计计算
1
2```python
3 def _reduce_output(output_list: np.ndarray):
4 """根据输出的状态序列,从初始值开始累加,形成一个(拟)价格序列
5
6 Args:
7 output_list (np.ndarray): 输出序列
8
9 Returns:
10 ndarray: (拟)价格序列
11 """
12 init_val = 1
13 # 从状态映射到涨跌幅。百分比。
14 price_map = {
15 0: -2, # large drop
16 1: -1.5, # drop
17 2: 0, # no change
18 3: 1.5, # small rise
19 4: 2 # large rise
20 }
21 enable_price_map = True
22 ret = np.zeros(len(output_list))
23 ret[0] = init_val
24 if enable_price_map:
25 for i in range(1, len(output_list)):
26 ret[i] = ret[i - 1] * (1 + price_map[output_list[i]] / 100)
27 else:
28 for i in range(1, len(output_list)):
29 ret[i] = ret[i - 1] + output_list[i] - 2
30 return ret
此时,结果就非常差了:
```python
acc_seq=
[0.28571429 0.14285714 0.28571429 0.17857143 0.57142857 0.07142857
0.25 0.21428571 0.10714286 0.28571429 0.03571429 0.21428571
0.25 0.03571429 0.03571429 0.28571429 0.28571429 0.28571429
0.28571429 0.28571429 0.39285714 0.10714286 0.28571429 0.07142857
0.28571429 0.32142857 0.25 0.25 0.32142857 0.21428571
0.25 0.14285714 0.10714286 0.03571429 0.21428571 0.28571429
0.28571429 0.25 0.25 0.14285714 0.03571429 0.32142857
0.28571429 0.28571429 0.28571429 0.07142857 0.17857143 0.21428571
0.10714286 0.28571429 0.25 0.28571429 0.07142857 0.17857143
0.10714286 0.14285714 0.03571429 0.10714286 0.28571429 0.32142857
0.14285714 0.17857143 0.28571429 0.25 0.28571429 0.28571429
0.10714286 0.53571429 0.35714286 0.10714286 0.28571429 0.28571429
0.07142857 0.28571429 0.21428571 0.03571429 0.07142857 0.28571429
0.25 0.07142857 0.03571429 0.25 0.32142857 0.14285714
0.17857143 0.14285714 0.10714286 0.17857143 0.17857143 0.17857143
0.17857143 0.32142857 0.10714286 0.10714286 0.03571429 0.32142857
0.10714286 0.28571429 0.14285714 0.28571429]
acc_seq.mean=
0.20714285714285713
acc_seq.std=
0.10630625761526584
精确度非常糟糕。
结论:考虑到观测值与测试错误在时间累加效应面前,会导致蝴蝶效应,导致预测准确率大大降低,无法用于指导购买股票。
学习、解题过程记录
我们先看看这个 mat 文件是啥东西。
1from scipy.io import loadmat
2mat = loadmat(file_mat, squeeze_me=True)
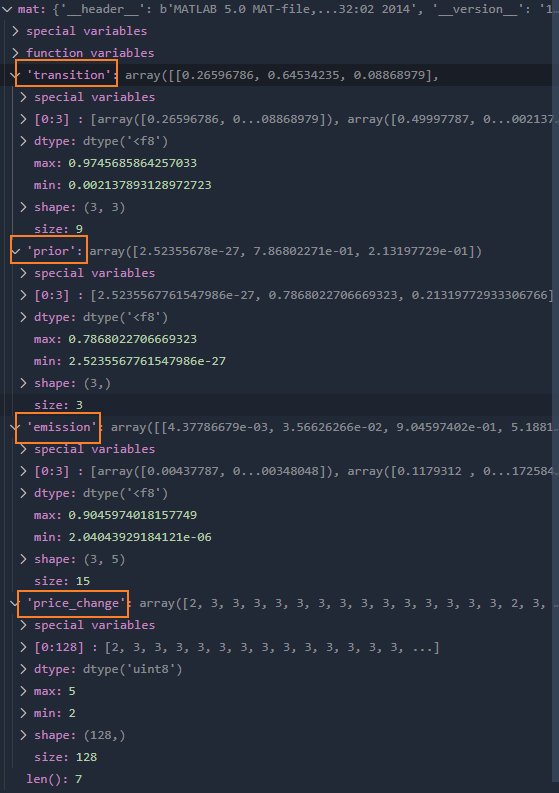
transition 是一个 3x3 的状态转移概率矩阵。描述了 i 状态下有 transition[i][j] 的概率转移到 j 状态。每个项称为 i 到 j 的转换概率。
在经典 Markov 模型中,将一个状态概率向量乘以这个矩阵,就得到下一个时刻的状态概率向量。
emission 是 3x3 的发射概率矩阵,也称 事件矩阵。它表明状态 i 下有 emission[i][j] 的概率观测到 j 的输出。这个输出就是前面说的 large drop 之类的东西。
prior 是一个 3x1 的初始状态概率向量,也叫初始概率分布或者状态的先验。prior[i] 表示系统启动时,有多大的概率以 i 状态开始。
price_change 是一个 128x1 的观测值数组,表示每个时间点的观测值。
整理一下得到:
1 # trans_bb[qi][qj] 表示状态 qi 转移到 qj 的概率
2 trans_bb = np.array(
3 [[0.26596786, 0.64534235, 0.08868979],
4 [0.49997787, 0.49788423, 0.00213789],
5 [0.02295626, 0.00247515, 0.97456859]]
6 )
7
8 # emit_bb[qi][oj] 表示状态 qi 下观测到 oj 的概率
9 emit_bb = np.array(
10 [[4.37786679e-03, 3.56626266e-02, 9.04597402e-01, 5.18816277e-02, 3.48047712e-03],
11 [1.17931200e-01, 2.36821594e-01, 2.51012581e-01,
12 2.21650346e-01, 1.72584279e-01],
13 [9.45849521e-03, 8.32174208e-02, 8.54638596e-01, 5.26834471e-02, 2.04043929e-06]]
14 )
15
16 # prior_bb[qi] 表示状态 qi 的先验概率。即初始取 qi 的概率。
17 init_pbb = np.array([2.52355678e-27, 7.86802271e-01, 2.13197729e-01])
18
19 # ob_seq[t] 表示第 t 个时刻的观测值
20 ob_seq = np.array([2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 3, 3, 3, 2, 3, 3,
21 3, 3, 3, 3, 3, 4, 3, 5, 4, 3, 3, 3, 2, 3, 4, 3, 2, 3, 4, 3, 3, 4,
22 3, 3, 3, 3, 3, 3, 3, 3, 2, 3, 3, 2, 3, 3, 3, 3, 3, 3, 2, 3, 3, 3,
23 3, 3, 3, 3, 2, 3, 3, 3, 4, 2, 5, 3, 3, 2, 3, 3, 3, 3, 4, 3, 3, 3,
24 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 3,
25 4, 3, 3, 4, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 4, 3, 3, 3], dtype=np.uint8)
26
27 # 因为索引从 0 开始,所以修正一下偏移量
28 ob_seq = ob_seq - 1
隐状态的计算:Forward-Backward 算法
要解决什么问题:给定 HMM,求解隐状态序列,即每个时间点,各隐状态的概率。
time 0 1 2 3 4 5 6 7 8 9 ... 128
p(q=0) ? ? ? ? ? ? ? ? ? ? ? ?
p(q=1) ? ? ? ? ? ? ? ? ? ? ? ?
p(q=2) ? ? ? ? ? ? ? ? ? ? ? ?
我们可以从 0 往右求,这样求 0~t 时间各隐状态的概率,称为前向概率或者正向概率。
也可以从 t 往右求,这样求 t~T 时间各隐状态的概率,称为后向概率或者反向概率。(注:约定 T 时刻表示最后时刻)
由于有关系 $\alpha_t(i)\beta_t(i)=P(i_t=q_i,O|\lambda) $,所以只要求出 $\alpha$ 和 $\beta$ 两个矩阵,就能求出状态序列。这两个矩阵的求解对应 Forward 和 Backward 算法。
Forward 算法
Forward 算法比较好理解,我们可以直接写出代码。
前向变量:$\alpha_t(j)$ 表示已知 $t$ 个时刻的观测序列,在 $t$ 时刻位于状态 $j$ 的概率。

当前是状态 i 的概率 prior[i],乘以状态 i 下输出 j 的概率 emission[i][j],得到的就是当前输出 j 的概率。
Forward DP 的实现如下:
1 def calc_forward_pbb(self, obs_seq: int):
2 """计算前向概率矩阵
3
4 Args:
5 obs_seq (int): 观测序列
6
7 Returns:
8 np.ndarrya: 前向概率矩阵,维度为 (n_states, len(obs_seq))
9 """
10 n_obs = len(obs_seq)
11 forward_pbb_mat = np.zeros((self.n_states, n_obs))
12 forward_pbb_mat[:, 0] = self.init_pbb * self.emit_pbb[:, 0]
13 for t in range(1, n_obs):
14 for i in range(self.n_states):
15 forward_pbb_mat[i, t] = np.dot(
16 forward_pbb_mat[:, t - 1], self.trans_pbb[:, i]
17 ) * self.emit_pbb[i, obs_seq[t]]
18
19 return forward_pbb_mat
其中关键点解释如下:
1forward_pbb_mat[i, t] =
2 np.dot(forward_pbb_mat[:, t - 1], self.trans_pbb[:, i]) # 表示时间前进一步之后产生状态 i 的概率
3 * self.emit_pbb[i, obs_seq[t]] # 表示状态 i 产生 t 对应的观测值的概率
4 # 二者相乘,表示时间前进一步之后,状态 i 产生观测值 obs_seq[t] 的概率
由于是一个马尔可夫过程,所以可以通过一步递推,forward_pbb_mat[i, t - 1] 推出 forward_pbb_mat[i, t]。顺着捋一遍之后就得到了整个序列各时刻的前向概率。
Backward 算法
后向概率:如果给定时刻 $t$,初态为 $q_i$ ,在此条件下,$t+1$ 到 $T$ 生成观测序列 $o_{t+1}, o_{t+2}, ..., o_{T}$ 的概率为 $\beta _t(i)$ ,则 $\beta _t(i)$ 称为后向概率。
如果要计算 $T-1$ 到 $T$ 的后向概率,$T-2$ 到 $T$ 的后向概率……势必会产生一些重复,所以也可以用 DP 的思想来“缓存”。
这次,我们是逆向递推。代码实现如下:
1 def calc_backward_pbb(self, ob_seq: list[int]):
2 """计算后向概率矩阵
3
4 Args:
5 ob_seq (list[int]): 观测序列
6 """
7 n_obs = len(ob_seq)
8 backward_pbb_mat = np.zeros((self.n_states, n_obs))
9 backward_pbb_mat[:, -1] = 1
10
11 for t in reversed(range(n_obs - 1)):
12 for i in range(self.n_states):
13 backward_pbb_mat[i, t] = np.sum(
14 backward_pbb_mat[:, t + 1] * self.trans_pbb[i, :] *
15 self.emit_pbb[:, ob_seq[t+1]]
16 )
17 return backward_pbb_mat
推导过程:
$$ \begin{align} \beta_{k}(z_k) &= P(x_{k+1:n} | z_k) \\ &= \sum_{z_{k+1}}P(x_{k+1:n},z_{k+1}|z_k) \\ &= \sum_{z_{k+1}}P(x_{k+1}, x_{k+2:n},z_{k+1}|z_k) \\ &= \sum_{z_{k+1}}P(x_{k+1}, x_{k+2:n}|z_{k+1}, z_k)P(z_{k+1}|z_k) \\ &= \sum_{z_{k+1}}P(x_{k+2:n}|z_{k+1}, z_k, x_{k+1})P(x_{k+1}|z_{k+1}, z_k)P(z_{k+1}|z_k) \\ \end{align} $$第一行,$\beta_k(z_k)$ 表示时间 $k$ ,状态 $z_k$ 的后向向量,即:当处于时间 $k$ 时,处于 $z_k$ 状态的概率。
第二行,我们将概率展开为一系列概率的和。每一项表示:当状态处于 $z_k$ 时,生成序列 $x_{k+1:n}$ 且下一个状态是 $z_{k+1}$ 的概率。为啥要求和?其实就是相当于遍历各个次态。也就是说,甭管是啥次态,但凡现态是 $z_k$,并且能产生这个序列,就算进来。
第三行,将生成序列拆成下一刻的,和下一刻之后的($x_k$, $x_{k+2:n}$ )
第四行,将次态放到条件,因此要乘以产生此次态的概率。
第五行,将产生下一个输出 $x_{k+1}$ 的概率放到条件。相应地乘以产生此输出的概率。
然后,利用条件独立性,化简为 $\sum_{z_{k+1}}\beta_{k+1}(z_{k+1})P(x_{k+1}|z_{k+1})P(_{k+1}|z_k)$
这也对应了核心部分的代码:
1backward_pbb_mat[i, t] = np.sum(
2 backward_pbb_mat[:, t + 1] * # 表示下一时刻的各状态后向概率
3 self.trans_pbb[i, :] * # 表示从 i 状态转移到其它状态的概率
4 self.emit_pbb[:, ob_seq[t+1]]# 表示发射出 t+1 时输出的概率
5)
Viterbi 算法
和 Forward 算法很类似。
1 def viterbi_decode(self, ob_seq: list[int]):
2 """计算隐藏状态序列(维特比路径)
3
4 Args:
5 ob_seq (list[int]): 观测序列
6 """
7 n_obs = len(ob_seq)
8 prev = np.zeros((n_obs - 1, self.n_states))
9
10 # 构造 DP 数组
11 # dp[i, t] 表示在 t 时刻,到达 i 状态的观测序列的最大概率
12 dp = np.zeros((self.n_states, n_obs))
13 dp[:, 0] = self.init_pbb * self.emit_pbb[:, ob_seq[0]]
14 for t in range(1, n_obs):
15 for i in range(self.n_states):
16 seq_pbb = dp[:, t-1] * self.trans_pbb[:, i] * \
17 self.emit_pbb[i, ob_seq[t]]
18 prev[t-1, i] = np.argmax(seq_pbb)
19 dp[i, t] = np.max(seq_pbb)
20
21 # 构造维特比路径
22 def build_viterbi_path(prev, last_state):
23 T = len(prev)
24 yield(last_state)
25 for i in range(T-1, -1, -1):
26 v = int(prev[i, last_state])
27 yield(v)
28 last_state = v
29
30 viterbi_path = np.array(list(build_viterbi_path(prev, np.argmax(dp[:, -1]))))
31 return viterbi_path
完整代码
1from matplotlib import pyplot as plt
2import numpy as np
3
4
5class HMM():
6
7 def __init__(self, trans_pbb: np.ndarray, emit_pbb: np.ndarray, init_pbb: np.ndarray):
8 """初始化隐马尔可夫模型
9
10 Args:
11 trans_pbb (np.ndarray): 转移概率矩阵
12 emit_pbb (np.ndarray): 输出概率矩阵
13 init_pbb (np.ndarray): 初始概率分布
14 """
15 self.trans_pbb = trans_pbb
16 self.emit_pbb = emit_pbb
17 self.init_pbb = init_pbb
18 self.n_states = len(init_pbb)
19
20 def calc_forward_pbb(self, ob_seq: list[int]):
21 """计算前向概率矩阵
22
23 forward_pbb_mat[i, t] 表示隐藏态为 i 条件下,在 0~t 时刻的前向概率。也即,经过 0~t 步,生成观测序列 ob_seq ,并最终落在 i 状态的概率。
24
25 Args:
26 ob_seq (list[int]): 观测序列
27
28 Returns:
29 np.ndarrya: 前向概率矩阵,维度为 (n_states, len(ob_seq))
30 """
31 n_obs = len(ob_seq)
32 forward_pbb_mat = np.zeros((self.n_states, n_obs))
33 forward_pbb_mat[:, 0] = self.init_pbb * self.emit_pbb[:, 0]
34 for t in range(1, n_obs):
35 for i in range(self.n_states):
36 forward_pbb_mat[i, t] = np.dot(
37 forward_pbb_mat[:, t - 1], self.trans_pbb[:, i]
38 ) * self.emit_pbb[i, ob_seq[t]]
39
40 return forward_pbb_mat
41
42 def calc_backward_pbb(self, ob_seq: list[int]):
43 """计算后向概率矩阵
44
45 backward_pbb_mat[i, t] 表示隐藏态为 i 条件下,在 t~T 时刻的后向概率。也即,从 i 状态开始,经过 t~T 步,生成观测序列 ob_seq 的概率。
46
47 Args:
48 ob_seq (list[int]): 观测序列
49 """
50 n_obs = len(ob_seq)
51 backward_pbb_mat = np.zeros((self.n_states, n_obs))
52 backward_pbb_mat[:, -1] = 1
53
54 for t in reversed(range(n_obs - 1)):
55 for i in range(self.n_states):
56 backward_pbb_mat[i, t] = np.sum(
57 backward_pbb_mat[:, t + 1] * self.trans_pbb[i, :] *
58 self.emit_pbb[:, ob_seq[t+1]]
59 )
60 return backward_pbb_mat
61
62 def viterbi_decode(self, ob_seq: list[int]):
63 """计算隐藏状态序列(维特比路径)
64
65 Args:
66 ob_seq (list[int]): 观测序列
67 """
68 n_obs = len(ob_seq)
69 prev = np.zeros((n_obs - 1, self.n_states))
70
71 # 构造 DP 数组
72 # dp[i, t] 表示在 t 时刻,到达 i 状态的观测序列的最大概率
73 dp = np.zeros((self.n_states, n_obs))
74 dp[:, 0] = self.init_pbb * self.emit_pbb[:, ob_seq[0]]
75 for t in range(1, n_obs):
76 for i in range(self.n_states):
77 seq_pbb = dp[:, t-1] * self.trans_pbb[:, i] * \
78 self.emit_pbb[i, ob_seq[t]]
79 prev[t-1, i] = np.argmax(seq_pbb)
80 dp[i, t] = np.max(seq_pbb)
81
82 # 构造维特比路径
83 def build_viterbi_path(prev, last_state):
84 T = len(prev)
85 yield(last_state)
86 for i in range(T-1, -1, -1):
87 v = int(prev[i, last_state])
88 yield(v)
89 last_state = v
90
91 viterbi_path = np.array(
92 list(build_viterbi_path(prev, np.argmax(dp[:, -1]))))
93 return viterbi_path
94
95
96def draw_state_trans(state_seq, fname):
97 seq_time = np.arange(len(state_seq))
98 fg, ax = plt.subplots(figsize=(10, 2))
99 ax.set(xlabel='time', ylabel='state', title='Hidden states')
100 state0 = np.ma.masked_where(state_seq == 0, state_seq)
101 state1 = np.ma.masked_where(state_seq == 1, state_seq)
102 state2 = np.ma.masked_where(state_seq == 2, state_seq)
103 ax.step(seq_time, state0, '-', label='state 0 (bear)')
104 ax.step(seq_time, state1, '-', label='state 1 (stable)')
105 ax.step(seq_time, state2, '-', label='state 2 (bull)')
106 ax.legend()
107 plt.savefig(fname)
108
109def draw_pbb_diagram(gamma, fname):
110 seq_time = np.arange(len(gamma[0]))
111 fg, ax = plt.subplots(figsize=(10, 2))
112 ax.set(xlabel='time', ylabel='probability', title='Probability Dist.')
113 state0data = gamma[0]
114 state1data = gamma[1]
115 state2data = gamma[2]
116 ax.plot(seq_time, state0data, '-', label='state 0 (bear)')
117 ax.plot(seq_time, state1data, '-', label='state 1 (stable)')
118 ax.plot(seq_time, state2data, '-', label='state 2 (bull)')
119 ax.legend()
120 plt.savefig(fname)
121
122
123def main():
124
125 # trans_bb[qi][qj] 表示状态 qi 转移到 qj 的概率
126 trans_bb = np.array(
127 [[0.26596786, 0.64534235, 0.08868979],
128 [0.49997787, 0.49788423, 0.00213789],
129 [0.02295626, 0.00247515, 0.97456859]]
130 )
131
132 # emit_bb[qi][oj] 表示状态 qi 下观测到 oj 的概率
133 emit_bb = np.array(
134 [[4.37786679e-03, 3.56626266e-02, 9.04597402e-01, 5.18816277e-02, 3.48047712e-03],
135 [1.17931200e-01, 2.36821594e-01, 2.51012581e-01,
136 2.21650346e-01, 1.72584279e-01],
137 [9.45849521e-03, 8.32174208e-02, 8.54638596e-01, 5.26834471e-02, 2.04043929e-06]]
138 )
139
140 # prior_bb[qi] 表示状态 qi 的先验概率。即初始取 qi 的概率。
141 init_pbb = np.array([2.52355678e-27, 7.86802271e-01, 2.13197729e-01])
142
143 # ob_seq[t] 表示第 t 个时刻的观测值
144 ob_seq = np.array([2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 3, 3, 3, 2, 3, 3,
145 3, 3, 3, 3, 3, 4, 3, 5, 4, 3, 3, 3, 2, 3, 4, 3, 2, 3, 4, 3, 3, 4,
146 3, 3, 3, 3, 3, 3, 3, 3, 2, 3, 3, 2, 3, 3, 3, 3, 3, 3, 2, 3, 3, 3,
147 3, 3, 3, 3, 2, 3, 3, 3, 4, 2, 5, 3, 3, 2, 3, 3, 3, 3, 4, 3, 3, 3,
148 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 3,
149 4, 3, 3, 4, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 4, 3, 3, 3], dtype=np.uint8)
150
151 # 因为索引从 0 开始,所以修正一下偏移量
152 ob_seq = ob_seq - 1
153
154 model = HMM(trans_bb, emit_bb, init_pbb)
155 ob_seq_100 = ob_seq[:100]
156 alpha = (model.calc_forward_pbb(ob_seq_100))
157 beta = (model.calc_backward_pbb(ob_seq_100))
158 print("alpha=")
159 print(alpha)
160 print("beta=")
161 print(beta)
162
163 # 通过求各时刻个状态的最大值,求状态序列
164 seq_gamma = alpha * beta
165 seq_gamma_argmax = np.argmax(seq_gamma, axis=0)
166 # 绘制
167 print("gamma=")
168 print(seq_gamma)
169 print("gamma(argmax)=")
170 print(seq_gamma_argmax)
171
172 draw_state_trans(seq_gamma_argmax, fname='problem_1.png')
173 draw_pbb_diagram(alpha * beta, fname='problem_1_2.png')
174
175 viterbi_seq = model.viterbi_decode(ob_seq_100)
176 print("viterbi_seq=")
177 print(viterbi_seq)
178 draw_state_trans(viterbi_seq, fname='problem_2.png')
179
180 def _reduce_output(output_list: np.ndarray):
181 """根据输出的状态序列,从初始值开始累加,形成一个(拟)价格序列
182
183 Args:
184 output_list (np.ndarray): 输出序列
185
186 Returns:
187 ndarray: (拟)价格序列
188 """
189 init_val = 1
190 # 从状态映射到涨跌幅。百分比。
191 price_map = {
192 0: -2, # large drop
193 1: -1.5, # drop
194 2: 0, # no change
195 3: 1.5, # small rise
196 4: 2 # large rise
197 }
198 enable_price_map = True
199 ret = np.zeros(len(output_list))
200 ret[0] = init_val
201 if enable_price_map:
202 for i in range(1, len(output_list)):
203 ret[i] = ret[i - 1] * (1 + price_map[output_list[i]] / 100)
204 else:
205 for i in range(1, len(output_list)):
206 ret[i] = ret[i - 1] + output_list[i] - 2
207 return ret
208 # 愚蠢的人类试图预测未来
209 n_seq = 28 # 预测长度
210 n_turn = 100 # 随机次数
211
212 # == 使用前向算法,估计最后一个状态的概率分布 ==
213 # 由于已经在前面调用过,所以我们直接使用 alpha 计算结果
214 alpha_last = alpha[:, 99]
215 output_real = ob_seq[100:128] # 实际值
216
217 # 最后状态。根据前向算法得出
218 forward_last_state = np.argmax(alpha_last)
219 price_seq_real = _reduce_output(output_real) # 真实价格序列
220 acc_seq = np.zeros(n_turn)
221 # 进行 n_turn 次模拟
222 for turn in range(n_turn):
223 last_state = forward_last_state
224 output_fit = np.zeros(n_seq) # 预测值
225 for t in range(n_seq):
226 # 按照状态转移概率分布,抽取一个状态
227 state = np.random.choice(
228 np.arange(3), p=model.trans_pbb[last_state])
229 # 按照此状态到各个观测值的概率,抽取一个观测值
230 output = np.random.choice(np.arange(5), p=model.emit_pbb[state, :])
231 output_fit[t] = output
232
233 last_state = state
234
235 price_seq_fit = _reduce_output(output_fit)
236 # # 计算拟合优度
237 # # -- 残差平方和 RSS
238 # ss_res = np.sum((price_seq_real - price_seq_fit) ** 2)
239 # # -- 总平方和 TSS
240 # ss_tot = np.sum((price_seq_real - np.mean(price_seq_real)) ** 2)
241 # # -- 拟合优度,伪平方和
242 # r2 = 1 - (ss_res / ss_tot)
243 # acc_seq[turn] = r2
244 from seqeval.metrics import accuracy_score
245 acc_seq[turn] = accuracy_score(output_real, output_fit)
246 # acc_seq[turn] = accuracy_score(price_seq_real, price_seq_fit)
247
248
249 # 输出拟合度的均值和标准方差
250 print("acc_seq=")
251 print(acc_seq)
252 print("acc_seq.mean=")
253 print(acc_seq.mean())
254 print("acc_seq.std=")
255 print(acc_seq.std())
256
257
258if __name__ == "__main__":
259 main()
参考
HMM(一):Graphical Model,HMM,Viterbi - 知乎 (zhihu.com)
HMM(二):Forward/Backward算法与参数估计 - 知乎 (zhihu.com)
隐马尔科夫模型(HMM)及其Python实现 | Javen Chen’s Blog (applenob.github.io)
