如何理解群的作用、轨道稳定子定理?
对于群作用可以基于定义理解。对于轨道稳定子定理可以从具体例子取理解证明思路。
左作用的定义
设 $X$ 是一个集合,$G$ 是一个群。$G$ 在 $X$ 上的一个左作用是一个映射 $G \times X \to X$,定义为 $(g, x) \mapsto gx$,满足以下条件:
-
单位元条件:对于
$X$中的任意元素$x$,有$e \cdot x = x$,其中$e$是群$G$的单位元。 -
结合性条件:对于
$G$中的任意元素$g, h$和集合$X$中的任意元素$x$,有$(gh) \cdot x = g \cdot (h \cdot x)$。
在这些条件下,$X$ 被称为一个 $G$-集。具体地说,$G$-集是一个集合 $X$ 配备了一个群 $G$ 的作用。
我们从定义来理解。
显然,群作用是一个映射 $G \times X \to X$,分析这个映射:
-
输入是一个群元素和一个集合元素的有序对
$(g, x)$。 -
输出是集合中的另一个元素
$g \cdot x$。
提醒, $X$ 和群的集合并不需要有什么必然关系。
-
可以看到群作用对于
$X$是封闭的。也就是说这个群中的任何元素,对操作数集合$X$上的任何元素进行运算,结果依然在$X$中。这意味着可以连续作用。 -
单位元性质意味着单位元对群的无作用。
-
结合性质意味着连续作用的顺序的无关性。
一个显然的例子是线性变换。
例子:矩阵乘法
设 $G = GL_2(\mathbb{R})$ 且 $X = \mathbb{R}^2$。
$G$ 通过左乘作用于 $X$。如果 $v \in \mathbb{R}^2$ 且 $I$ 是单位矩阵,则 $Iv = v$。如果 $A$ 和 $B$ 是 $2 \times 2$ 的可逆矩阵,则 $(AB)v = A(Bv)$,因为矩阵乘法是结合的。
取一个非常具体的例子,如果 $X$ 是一个正方形的顶点集合:
$$
\text{square} = \begin{bmatrix} 1 & -1 & -1 & 1 \\ 1 & 1 & -1 & -1 \end{bmatrix}
$$
(注意 $X$ 和 $G$ 中元素(矩阵)大小并不相同,一个是 2x4,一个是 2x2), $G$ 是 $\text{GL}(2)$ 中的旋转矩阵:
$$
R(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}
$$
群作用很显然就是代表对顶点进行不同角度的旋转,单位元的角度是 0,即单位阵。旋转变换显然是顺序无关的。例如我们进行 5, 15, 45 度旋转:
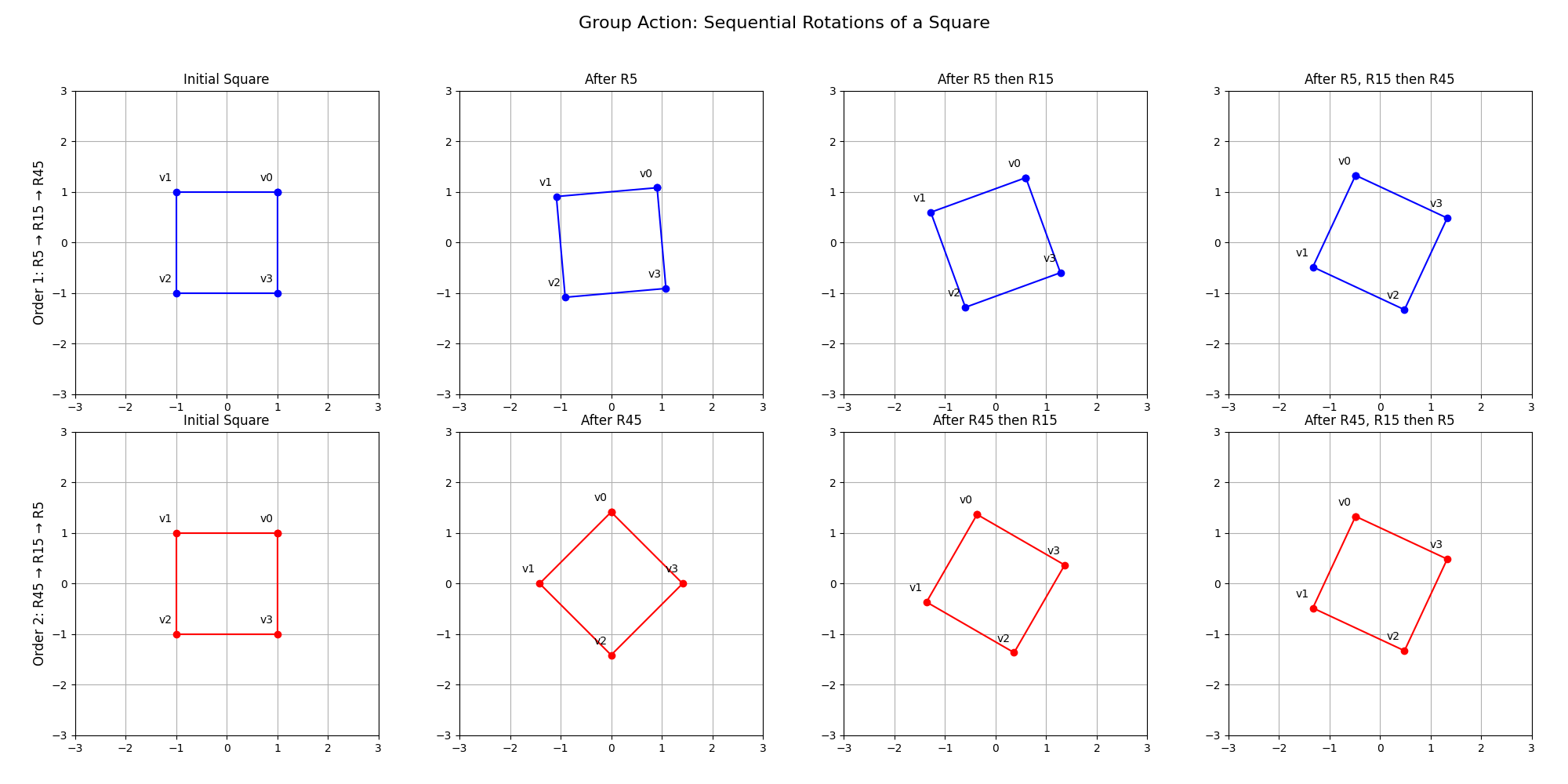
尽管群作用的顺序不同,但最终得到相同的结果。
当
实际上当 $X = G$ 时,即,对于 $g \in G$,定义映射 $\lambda_g: G \to G$ 为 $\lambda_g(x) = gx$。这个时候左作用于自身,叫做左正则表示,自作用。
作为 $GL(2)$ 中的元素,上面的三个旋转矩阵可以先进行自作用,合成为一个旋转65 度的旋转矩阵,然后再和 X 集合作用,效果相同。
轨道
如果 $X$ 是一个 $G$-集(即群 $G$ 作用在集合 $X$ 上),那么对于 $x \in X$,轨道是由 $G$ 中的元素作用于 $x$ 所得到的所有结果组成的集合。
具体来说,轨道 $\text{Orb}_G(x)$ 定义为:
$$
\text{Orb}_G(x) = \{ g \cdot x \mid g \in G \}
$$
这里 $g \cdot x$ 表示群 $G$ 的元素 $g$ 作用在 $X$ 中的元素 $x$ 上所得到的结果。轨道表示了在群作用下,元素 $x$ 可以被移动到的所有位置。
举例来说,如果 $X$ 是一个正方形的顶点集合,$G$ 是所有的旋转矩阵,轨道 $\text{Orb}_G(v)$ 是通过对所有可能的旋转角度应用 $R(\theta)$ 得到的点集。
我们首先绘制出所有可能的变换后情况(这里为了便于辨认只画了一些离散的点)
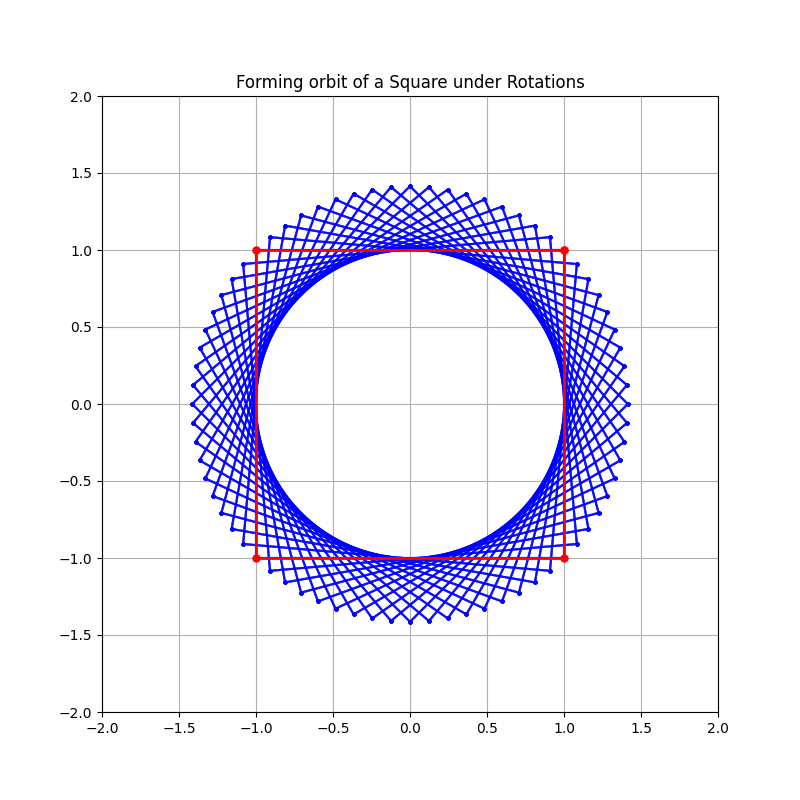
所有顶点的轨迹会形成一个半径为 $\sqrt{2}$ 的圆。
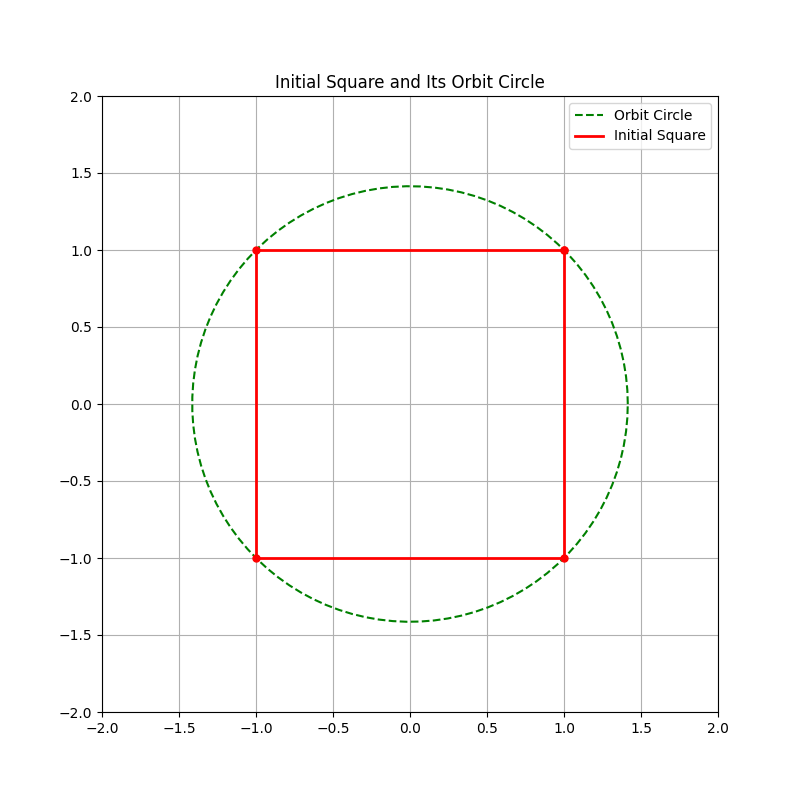
由于正方形在 $90^\circ$ 的倍数旋转下会得到自身,所以轨道实际上是正方形的所有旋转对称位置。具体来说,轨道包含以下旋转:
-
$0^\circ$(原始位置) -
$90^\circ$ -
$180^\circ$ -
$270^\circ$
因此,轨道是正方形在这些旋转下的所有可能位置集合。每个顶点在这些旋转下的位置会形成一个循环,反映出正方形的对称性。
轨道-稳定子定理
轨道-稳定子定理是群作用中的一个重要结果。它描述了群作用下轨道和稳定子之间的关系。
对于一个群 $G$ 作用在集合 $X$ 上,给定 $x \in X$,定义稳定子 $\text{Stab}_G(x)$:群 $G$ 中使 $x$ 不变的元素集合,即 $\{ g \in G \mid g \cdot x = x \}$。
轨道-稳定子定理指出:
$$
|G| = |\text{Orb}_G(x)| \cdot |\text{Stab}_G(x)|
$$
其中 $|G|$ 是群 $G$ 的阶,$|\text{Orb}_G(x)|$ 是轨道的大小,$|\text{Stab}_G(x)|$ 是稳定子的大小。
-
轨道的大小 表示了一个元素在群作用下可以移动到多少个不同的位置。
-
稳定子的大小 表示了群中有多少个元素在不改变该元素位置的情况下依然保持原样。
-
群的阶 则等于轨道大小与稳定子大小的乘积,反映了群的整体结构如何通过其对特定元素的作用分解。
举例
对于 $\text{GL}(2)$ 中的旋转变换(这里只考虑绕原点旋转变换,即上面给出的矩阵),原点的稳定子就是整个旋转群,因为所有旋转都保持原点不变。
然而,考虑到旋转矩阵有无穷个,我们举一个有限群的例子:
考虑一个正方形的对称群 $D_4$,它包含旋转和反射。具体包括:
-
恒等元素:
$e$ -
旋转元素:
-
$r$:顺时针旋转 90° -
$r^2$:顺时针旋转 180° -
$r^3$:顺时针旋转 270°
-
-
反射元素:
-
$s$:关于一条对称轴的反射 -
$sr$:关于另一条对称轴的反射 -
$sr^2$:关于第三条对称轴的反射 -
$sr^3$:关于第四条对称轴的反射
-
这些元素构成了 $D_4$ 的完整集合。取正方形的一个顶点 $v_0$:
-
$|\text{Orb}_{D_4}(v_0)| = 4$,因为在不同旋转和反射下,顶点可以到达正方形的四个顶点位置。 -
$|\text{Stab}_{D_4}(v_0)| = 2$,因为只有恒等变换和沿该顶点的对称轴反射不改变顶点的位置。
代入轨道-稳定子定理:
$$
|D_4| = 8 = 4 \times 2
$$
得验,说明轨道-稳定子定理在此具体情形下是成立的。
如何从这个例子直观理解这个定理呢?
很简单,站在任何一个顶点的角度,有两种作用是稳定的:
-
恒等。保持原位。
-
穿过此顶点的轴的对称。依然保持原位。
在这两种作用 $\{ e,s \}$ 的基础上,施加 8 个作用。这 8 个作用一定可以会被分 4 个等价类。原因是拉格朗日定理。
可以手动验算:
-
$e\{e, s\} = \{e, s\}$ -
$r\{e, s\} = \{r, rs\}$ -
$r^2\{e, s\} = \{r^2, r^2s\}$ -
$r^3\{e, s\} = \{r^3, r^3s\}$ -
$s\{e, s\} = \{s, e\} = \{e, s\}$(与第一个相同) -
$sr\{e, s\} = \{sr, r\}$(与第二个相同) -
$sr^2\{e, s\} = \{sr^2, r^2\}$(以此类推) -
$sr^3\{e, s\} = \{sr^3, r^3\}$(以此类推)
化简后:
-
$\{e, s\}$ -
$\{r, rs\}$ -
$\{r^2, r^2s\}$ -
$\{r^3, r^3s\}$
这实际上就是稳定子的左陪集。这种划分实际上定义了一种 等价关系:两个群元素 $g$ 和 $h$ 是等价的,当且仅当它们在某个轨道内,即存在一个群元素 $k$ 使得 $g = k \cdot h$。
因此,每个等价类对应于一个轨道,反映了群元素在不同轨道和稳定子之间的分配情况。具体来说,每个元素都有两个稳定子,这两个稳定子每个形成四个轨道。因此证明此定理时就可以沿用这个思路。
证明:
-
定义
$G$上的等价关系$\sim$,两个群元素等价当且仅当它们对$x$的作用结果相同:$$ g_1 \sim g_2 \iff g_1 \cdot x = g_2 \cdot x $$- 对于某个
$x \in X$,假设$g \in G$是任意元素。等价类可以表示为:
$$ [g] = \{ h \in G \mid h \cdot x = g \cdot x \} $$注意到如果
$h \cdot x = g \cdot x$,则$h^{-1}g \cdot x = x$,即$h^{-1}g \in \text{Stab}_G(x)$。则:$$ [g] = g \cdot \text{Stab}_G(x) = \{ g s \mid s \in \text{Stab}_G(x) \} $$即每个等价类是稳定子
$\text{Stab}_G(x)$的一个左陪集。 - 对于某个
-
由等价关系的定义可知,群
$G$被其左陪集$g \cdot \text{Stab}_G(x)$完全划分。不同的等价类(陪集)对应于不同的轨道中的元素。 -
根据拉格朗日定理,群
$G$的阶等于一个陪集的大小乘以陪集的个数。这里,一个陪集的大小即$|\text{Stab}_G(x)|$,而陪集的个数等于轨道的大小$|\text{Orb}_G(x)|$。因此:
$$ |G| = |\text{Orb}_G(x)| \times |\text{Stab}_G(x)| $$
相关代码:
1import numpy as np
2import matplotlib.pyplot as plt
3
4def rotation_matrix(theta):
5 return np.array([[np.cos(theta), -np.sin(theta)],
6 [np.sin(theta), np.cos(theta)]])
7
8def apply_group_action(matrix, points):
9 return matrix @ points
10
11# Define initial square points (square centered at origin)
12square = np.array([[1, -1, -1, 1, 1],
13 [1, 1, -1, -1, 1]]) # Closing the square by returning to the first point
14
15# Define distinct rotation angles (degrees converted to radians)
16angles_deg = [5, 15, 45]
17angles_rad = [np.deg2rad(angle) for angle in angles_deg]
18
19# Create rotation matrices
20rot_matrices = [rotation_matrix(theta) for theta in angles_rad]
21
22# Define two different orders of applying the rotations
23order1 = [rot_matrices[0], rot_matrices[1], rot_matrices[2]]
24order2 = [rot_matrices[2], rot_matrices[1], rot_matrices[0]]
25
26def sequential_transformations(initial_points, rotation_order):
27 transformed_points = [initial_points]
28 current_points = initial_points.copy()
29 for matrix in rotation_order:
30 current_points = apply_group_action(matrix, current_points)
31 transformed_points.append(current_points)
32 return transformed_points
33
34# Apply transformations in both orders
35transforms_order1 = sequential_transformations(square, order1)
36transforms_order2 = sequential_transformations(square, order2)
37
38# Visualization parameters
39fig, axes = plt.subplots(2, 4, figsize=(20, 10))
40
41# Titles for the subplots
42titles = [
43 "Initial Square",
44 "After R5",
45 "After R5 then R15",
46 "After R5, R15 then R45"
47]
48
49# Plot for Order 1
50for i in range(4):
51 ax = axes[0, i]
52 transformed = transforms_order1[i]
53 ax.plot(transformed[0], transformed[1], 'b-', marker='o')
54 ax.set_title(titles[i])
55 ax.set_xlim(-3, 3)
56 ax.set_ylim(-3, 3)
57 ax.set_aspect('equal')
58 ax.grid(True)
59 # Label vertices
60 for j, txt in enumerate(['v0', 'v1', 'v2', 'v3']):
61 ax.annotate(txt, (transformed[0, j], transformed[1, j]), textcoords="offset points", xytext=(-10,10), ha='center')
62
63# Titles for the second row
64titles_order2 = [
65 "Initial Square",
66 "After R45",
67 "After R45 then R15",
68 "After R45, R15 then R5"
69]
70
71# Plot for Order 2
72for i in range(4):
73 ax = axes[1, i]
74 transformed = transforms_order2[i]
75 ax.plot(transformed[0], transformed[1], 'r-', marker='o')
76 ax.set_title(titles_order2[i])
77 ax.set_xlim(-3, 3)
78 ax.set_ylim(-3, 3)
79 ax.set_aspect('equal')
80 ax.grid(True)
81 # Label vertices
82 for j, txt in enumerate(['v0', 'v1', 'v2', 'v3']):
83 ax.annotate(txt, (transformed[0, j], transformed[1, j]), textcoords="offset points", xytext=(-10,10), ha='center')
84
85# Overall titles
86axes[0,0].set_ylabel('Order 1: R5 → R15 → R45', fontsize=12)
87axes[1,0].set_ylabel('Order 2: R45 → R15 → R5', fontsize=12)
88
89plt.suptitle('Group Action: Sequential Rotations of a Square', fontsize=16)
90plt.tight_layout(rect=[0, 0.03, 1, 0.95])
91plt.show()
