把“不同的子序列”问题说透彻

一些废话

网上题解数不胜数，但是凭什么他就能知道递推关系？就仿佛魔法一样从天上掉了下来，妙手偶得一般。会用、会写，但不能自己_重新发现_，不是工程师的掌握知识的态度。

动态规划，说白了就是数学归纳。最难的地方在于发现规律，而不是把规律描述下来。与其掌握抽象描述，不如从例子入手。

下面是例子。

一些规定

设关系 $R(s,t)$ 表示 S 的所有子序列中，等于 T 的子序列的个数

设递推关系 $f(i,j)$ 为 $R(s[0:i],t[0:i])$

一个例子

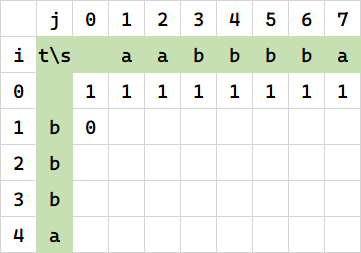
首先初始化，前置空串，这都是常用套路：

继续填写，出现了第一个 1：

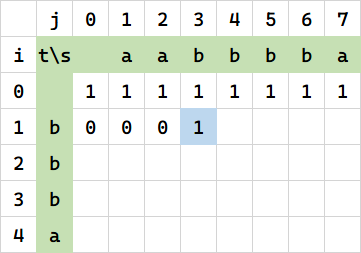
这是因为 R(aa, b) = 0，而 R(aab, b) 第一次出现了 b。可以发现原本不能匹配的，加上了 b 可以匹配了。

继续操作。有意思的来了：

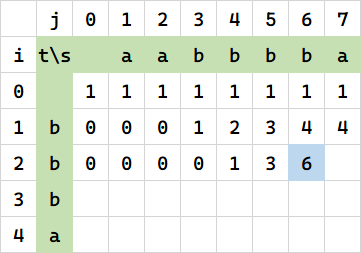
你看，这个 6 是怎么来的？我是这么算的：

计算 R(aabbbb, bb)，相当于 $C_4^2 = 6$，四个 b 里头选两个 b。

好，这时候观察周围的单元格又是怎么来的。

左边 3，是因为 $C_3 ^2 = 3$。
左上 3，是因为 $C_3^1 = 3$
正上 4，是因为 $C_4^1 = 4$

这让我想到了组合数的递推公式：$C_n ^k = C_{n-1}^{k-1} + C_{n-1}^k$

你看：$C_4^2 = C_3^1 + C_3^2$，这不就对上了。

也即：当 s[j] == t[i] 时，$f(i,j) = f(i-1,j-1)+f(i, j-1)$

接着往后算：

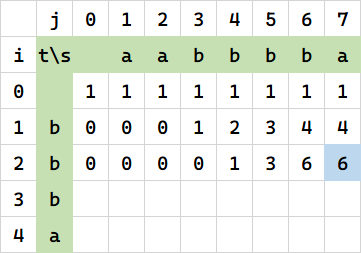
这个 6 又是怎么来的呢？R(aabbbba,bb) = 6，是因为后面多的这个 a 啊，它对结果不会造成任何影响，因为和 t 没法匹配。为啥没法匹配？因为结尾字符不同，对不上。所以就只能删掉这个 a，看能匹配多少。那不就是 R(aabbbb, bb)，也就是它左边那个。即只能往左边继承。

我们发现：

如果代表串末尾字符不相等，那么就只能删掉这个字符。相当于它左边的格子。

当 s[j] == t[i] 时，$f(i,j) = f(i, j-1)$
如果代表串末尾字符相等，那么一方面左边的格子可以继承，另一方面也还要加上左上方的格子。这是组合数的递推公式决定的。

当 s[j] == t[i] 时，$f(i,j) = f(i-1,j-1)+f(i, j-1)$

组合数递推公式

组合数的递推公式是怎么来的？

（此处例子来自排列组合的一些公式及推导(非常详细易懂) - 樱花赞 - 博客园 (cnblogs.com)）

从 $S=\{1,2,3,4,5\}$ 中选择两个，有以下情况：

12 13 14 15, 23 24 25, 34 35, 45

其中含有 1 的有 4 个，即12 13 14 15。这等价于从 2 3 4 5 个里面挑一个，即 $C_4^1$

不含有 1 的有 6 个，即 23 24 25, 34 35, 45，这等价于从 2, 3, 4, 5 里面挑两个，即 $C_4^2$

这个例子中 $C_5^2 = C_4^1 + C_4^2$，我们推而广之有：

$$ C_n ^k = C_{n-1}^{k-1} + C_{n-1}^k $$

你喜欢的话，也可以写成：

$$ f(i,j) = f(i-1,j-1)+f(i, j-1) $$

回到例子

如果代表串末尾字符相等，那么一方面左边的格子可以继承，另一方面也还要加上左上方的格子。这是组合数的递推公式决定的。

当 s[j] == t[i] 时，$f(i,j) = f(i-1,j-1)+f(i, j-1)$

现在，可以更有把握地说：$f(i,j)$ 的确切递推含义是：

$s[0:j]$ 中包含 $t[0:i]$ 的子序列情况，要么涉及了 $s[j]$，要么不涉及。

如果涉及，数量是 $f(i,j-1)$ （即例子中求 R(aabbbba, bb)，相当于求 R(aabbbb, bb) ）
如果不涉及，则数量是 $f(i-1,j-1)$. （即例子中求 R(aabbbb, b)）