自动机的幂集构造法详解

幂集构造，又叫子集构造，是一种将 NFA 转换为 DFA 的算法。下面通过一个例子学习。

【例子】 这是识别 101 结尾的二进制串的 NFA。将其转换为 DFA。

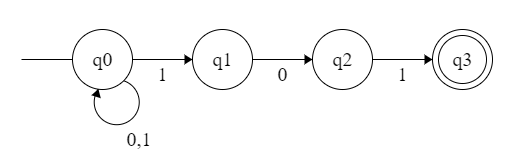
分析：

NFA 的状态转移表：

				0			1
->	{q0}		{q0}		{q0,q1}
	{q1}		{q2}		/
	{q2}		/			{q3}
*	{q3}		/			/

我们逐行看，第一行产生了新的状态 {q0,q1}。考察这个状态的两个子状态 q0, q1。

当输入 0 时：

• {q0} 跳至 {q0}

• {q1} 跳至 {q2}

所以我们有：

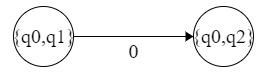
同理，输入 1 时有：

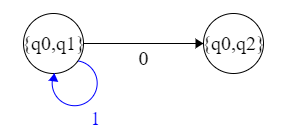
据此在状态转移表添加一行 {q0,q1}，得到：

				0			1
->	{q0}		{q0}		{q0,q1}
	{q1}		{q2}		/
	{q2}		/			{q3}
*	{q3}		/			/
	{q0,q1}		{q0,q2}		{q0,q1}

重复这样的操作（称为子集构造），得到：

				0			1
->	{q0}		{q0}		{q0,q1}
	{q1}		{q2}		/
	{q2}		/			{q3}
*	{q3}		/			/
	{q0,q1}		{q0,q2}		{q0,q1}
	{q0,q2}		{q0}		{q0,q1,q3}
*	{q0,q1,q3}	{q0,q2}		{q0,q1}

注：最初接受状态是 {q3}，则要把所有构造出的含有 q3 的状态标记为接受。

重命名，得到：

			0		1
->	s0		s0		s4
	s1		s2		/
	s2		/		s3
*	s3		/		/
	s4		s5		s4
	s5		s0		s6
*	s6		s5		s4

从而得到如下的状态机：

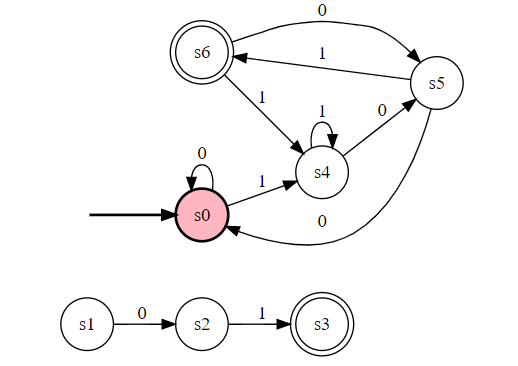
可以看到有三个冗余状态 s1, s2, s3。

所以一般而言（尤其对于复杂的 DFA），我们还要通过 DFA 的最小化技术消去无用的状态。