数字签名原理:从 Lamport 到椭圆曲线
签名
和现实世界的签名一样,数字签名解决的主要问题是认证和不可否认性。
-
认证:证明是你签的
-
不可否认:你不能抵赖说不是你签的
主要原语:
-
密钥生成:
$\mathrm{KeyGen}(1^k) \rightarrow (pk, sk)$- 输入安全参数
$k$,输出公钥$pk$和私钥$sk$
- 输入安全参数
-
签名生成:
$\mathrm{Sign}(sk, m) \rightarrow \sigma$- 输入私钥
$sk$和消息$m$,输出签名$\sigma$
- 输入私钥
-
签名验证:
$\mathrm{Verify}(pk, m, \sigma) \rightarrow \{0, 1\}$- 输入公钥
$pk$、消息$m$和签名$\sigma$,输出$1$表示验证通过,$0$表示验证失败
- 输入公钥
Lamport 签名
只用哈希就能实现签名!
密钥生成
首先生成私钥。下面的是 $2\times 256$ 数组,且每个元素(小方块)都是 32 Bytes。里面随即填充数据。

然后生成公钥。很简单,哈希所有元素,然后填充到新的相同形状数组。然后我们得到了公钥,也就是所有的绿色方块。
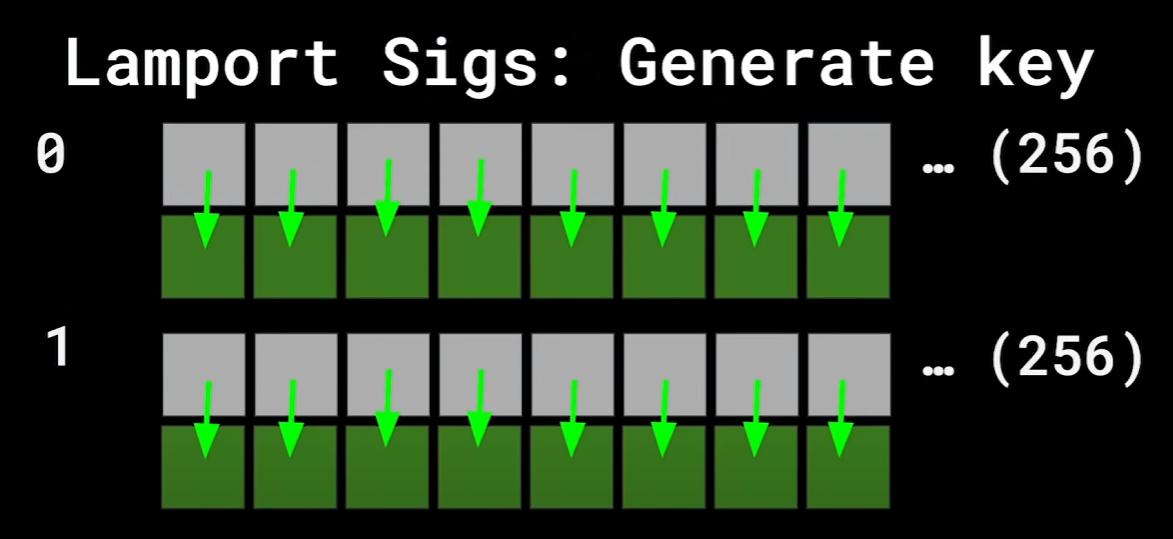
签名生成
假设要对 $m$ 签名,我们先 SHA256 哈希,得到 $h(m)$,它的二进制形式可能是 $01101110\cdots$,然后根据每一位是 0 还是 1,选择第 0 或第 1 组私钥来签名(哈希)。

这些哈希构成了签名的内容。
签名验证
把这些对应的私钥块揭露给验证者。验证者分块分别哈希,看看是不是等于公钥。这样就完成了验证。

总结:
-
密钥生成:生成两对密钥(sk和pk各一对):私钥sk是随机生成的,公钥pk则是私钥的哈希值。这样,每个位都有两种可能的私钥和公钥,形成一个两层的密钥结构。
-
签名:根据消息哈希的每一位选择相应的私钥;
-
验证:用公钥和哈希值确认签名的有效性。
代码实现
1import hashlib
2import secrets
3
4sk = [[None for _ in range(256)] for _ in range(2)]
5pk = [[None for _ in range(256)] for _ in range(2)]
6for i in range(256):
7 sk[0][i] = secrets.token_bytes(32)
8 sk[1][i] = secrets.token_bytes(32)
9 pk[0][i] = hashlib.sha256(sk[0][i]).digest()
10 pk[1][i] = hashlib.sha256(sk[1][i]).digest()
11
12raw = b'The quick brown fox jumps over the lazy dog'
13msg = int.from_bytes(hashlib.sha256(raw).digest(), 'little')
14sig = [None for _ in range(256)]
15for i in range(256):
16 b = msg >> i & 1
17 sig[i] = sk[b][i]
18
19for i in range(256):
20 b = msg >> i & 1
21 assert hashlib.sha256(sig[i]).digest() == pk[b][i]
缺点
-
一次性。生成签名需要泄露一部分私钥。如果私钥全部泄露,攻击者就可以伪造任意消息的签名。
-
有点大。8KiB sig, 16KiB pri/pub key
改进 Lamport 签名
我们有两个公钥,可以使用两次。(注意,这里使用两次只是指可以在揭露前,进行两次签名,但一旦揭露私钥之后,就不可再使用)
如何改进一次性签名方案?有一种办法,可以只使用 32 bytes 的私钥(而不是 16KB)就能产生 2x256 个公钥。原理很简单:
pub[i][j] = hash(seed, i, j)

这样我们减少了私钥大小(但是公钥大小翻倍),使用过程如下:
密钥生成
-
私钥是一个 32 字节的种子值
seed -
公钥是使用
seed和索引i,j计算出来的 256 个公钥值:pub[i][j] = h(seed, i, j) # i in {0,1}, j in {0, ..., 255} -
总共生成 2 * 256 = 512 个公钥值
签名生成
-
对于需要签名的 256 位消息摘要
01101110..., 按位检查每个比特位: -
如果比特位为 0, 则使用
pub[0][j]作为签名的一部分 -
如果比特位为 1, 则使用
pub[1][j]作为签名的一部分 -
将所有 256 个公钥值作为签名输出
签名验证
-
接收方使用公钥种子
seed重新计算出所有 512 个公钥值 -
对于收到的签名, 按位检查每个比特位:
-
如果比特位为 0, 则检查对应的
pub[0][j]是否与签名中的值匹配 -
如果比特位为 1, 则检查对应的
pub[1][j]是否与签名中的值匹配 -
如果所有比特位的验证都通过, 则认为签名有效
多次签名
这种方法可以扩展,只要尚未揭露私钥。我们可以生成很多组公钥用于签名。
问题
如果要签名四次,那么一共要生成 64 KB 的公钥。 随着签名次数的增大,需要在本地存储线性级别增长的公钥。并且对于每个验证者,都需要向他出示之前生成过的所有公钥。
解决方法是 Merkle 树。
RSA
一种未在加密货币领域使用的对称加密算法。
盲签名
支持盲签名(即在内容不揭露的情况下签名),过程如下:
-
$m' = m + r$对原始消息 添加一个随机数得到一个新的消息 。对消息进行随机化的方法,目的是为了提高签名的安全性。 -
$\mathrm{sig} (m') = s'$对修改后的消息进行签名,得到签名值 。签名算法可以是 RSA 签名、ECDSA 签名等。 -
$s = s' - r$通过减去之前添加的随机数 ,得到最终的签名值 。- 这样做的目的是为了保证签名值
$s$与原始消息$m$的签名一致,即$\mathrm{sig}(m) = s$。
- 这样做的目的是为了保证签名值
这个过程中,签名的人不会知道它签的原始消息是什么。
签名生成
RSA 算法的 setup 步骤如下:
-
选择两个大素数
$p$和$q$。 -
计算
$n = p \times q$。素数性质保证很难找到$n$的 preimage。 -
计算
$\phi(n) = (p-1)(q-1)$, 其中$\phi(n)$是 Euler 函数。 -
选择一个整数
$e$, 使得$1 < e < \phi(n)$且$\gcd(e, \phi(n)) = 1$。通常选择$e = 65537$,或者$3$。这个数可以公开。 -
计算
$d$使得$d \times e \equiv 1 \pmod{\phi(n)}$。这可以通过扩展欧几里得算法来实现。或者写作$d=e^{-1} \bmod (p-1) \times(q-1)$
此时,公钥为 $(e, n)$,私钥为 $(d, n)$. $p, q$ 可以丢掉。
在 RSA 算法中,签名和验证的过程如下:
签名
- 使用私钥
$(d, n)$对消息$m$进行签名:
$$
s = m^d \mod n
$$
其中 $s$ 就是签名结果。
验证
- 使用公钥
$(e, n)$对签名$s$进行验证:
$$
m' = s^e \mod n
$$
- 比较
$m'$和原始消息$m$是否相等。如果相等,则说明签名有效,否则签名无效。
具体步骤如下:
-
发送者使用自己的私钥对消息
$m$进行签名,得到签名$s$。 -
接收者使用发送者的公钥对签名
$s$进行验证,得到$m'$。 -
如果
$m' = m$,则说明签名有效,消息未被篡改。
这样可以确保消息的完整性和来源的真实性。
EC
Bitcoin 使用 $y^2=x^3+7$,在曲线上画一条割线,交于 $P,Q,-R$,满足 $P+Q-R=0$,则 $-R$ 的对称点满足 $R=P+Q$
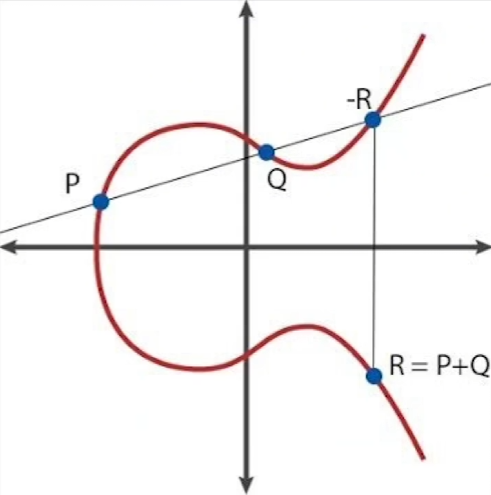
实际计算时,计算机处理的是模运算,保持了一些性质,但曲线不会像上面这么好看。
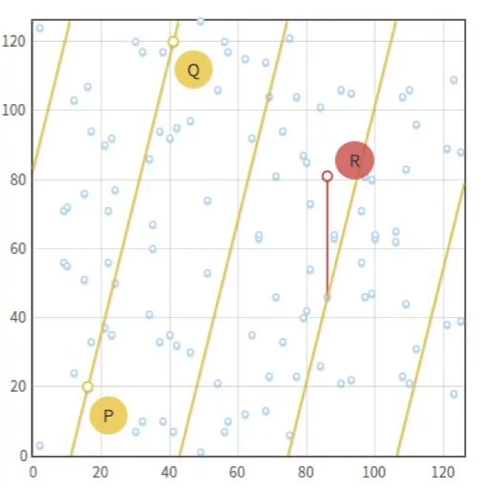
椭圆曲线上的点运算
在椭圆曲线上,有三种基本的点运算:
-
点加法 (Point Addition):
-
给定两个不同的点
$P(x_1, y_1)$和$Q(x_2, y_2)$,计算它们的和$R = P + Q$。 -
计算方法是:
-
计算斜率
$\lambda = (y_2 - y_1) / (x_2 - x_1)$ -
计算
$x_R = \lambda^2 - x_1 - x_2$ -
计算
$y_R = \lambda(x_1 - x_R) - y_1$
-
-
结果为
$R(x_R, y_R)$。
-
-
点倍乘 (Scalar Multiplication):
-
给定一个点
$P(x, y)$和一个整数$k$,计算$Q = k \cdot P$。 -
计算方法是重复进行点加法:
-
$Q = P$ -
对于
$i = 2$到$k$,$Q = Q + P$
-
-
结果为
$Q(x_Q, y_Q)$。
-
-
点求负 (Point Negation):
-
给定一个点
$P(x, y)$,计算其负点$-P(x, -y)$。 -
负点的
$y$坐标取相反数,$x$坐标不变。
-
几何意义:
-
点加法 (
$P + Q$): 对于曲线上的两个点$P$和$Q$,作过这两点的直线与曲线的第三个交点,然后以这个交点关于$x$轴对称的点作为$P + Q$的结果。 -
点倍乘 (
$k \cdot P$): 对于曲线上的一个点$P$,作过$P$的切线与曲线的第二个交点,然后以这个交点关于$x$轴对称的点作为$2 \cdot P$的结果。重复这一过程$k$次,即可得到$k \cdot P$的结果。 -
点相反 (
$-P$): 对于曲线上的一个点$P$,以$P$关于$x$轴对称的点作为$-P$的结果。
椭圆曲线中点的加法满足交换律,即 $aB = bA$。
推导如下:由于加法满足交换律,所以有 $aB = a(bG) = (ab)G = b(aG) = bA$。因此,无论先将 $G$ 点乘以 $a$ 再乘以 $b$,还是先乘以 $b$ 再乘以 $a$,结果都是相同的。
密钥生成
-
随机生成一个大整数
$a$,作为用户的私钥。- 一般选择一个 256 位的标量。
-
计算公钥
$A = a \cdot G$,其中$G$是椭圆曲线$y^2 = x^3 + 7$上的随机选取的基点(生成点,Generator Point)。-
$x_{A},y_{A}$都是 32 bytes 整数,因此一共需要 64 bytes 空间存储公钥。 -
考虑到曲线是关于
$x$轴对称的,可以压缩到 33 bytes, 其中一个 byte 用来指示是在正半轴还是负半轴。
-
签名生成
-
随机生成一个整数
$k$,作为签名的随机数。$k$相当于一个新的随机私钥。 -
计算
$R = k \cdot G = (x_R, y_R)$。 -
计算
$s = k^{-1} \cdot (m + a \cdot x_R) \mod n$,其中$m$是待签名的消息哈希值,$n$是椭圆曲线的阶。-
这个公式是原始 DSA 形式
-
$s = k - h(m,R)a$是 ECDSA 形式变 -
签名结果为
$(x_R, s)$。
-
签名验证
验证过程如下:
-
计算
$sG$ -
计算
$h(m, R)A$,其中$A$是签名者的公钥 -
验证等式
$sG = R - h(m, R)A$是否成立
原理解释:
-
私钥
$a$和公钥$A$满足$A = aG$ -
将签名等式两边同时乘以
$G$,利用$A = aG$,可以得到验证等式
$$
\begin{aligned}
sG &= (k - h(m,R)a)G \\
&= kG - h(m,R)aG \\
&= R - h(m,R)A
\end{aligned}
$$
因此只需要判断 $R == sG + h(m,R)A$
所以验证等式其实就是签名等式乘以基点 $G$ 得到的。签名过程只有持有私钥 $a$ 的签名者才能完成,而任何人都可以用公钥 $A$ 进行验证。
密钥交换
考虑 $A=aG, B=bG, aB = bA = C$,$C$ 称为 Diffie Hellman 密钥交换点。我们可以用 $C$ 作为共享的公共密钥,在信道中不会传输 $C$,而是各自通过公开信息计算出来(比如对于 A 方而言,通过 $bA$ 来计算),因此可以加密内容并安全地交换。
密钥组合
在 ECC 中,可以将两个密钥组合成一个新的密钥(Key Combination)。
原理
设 $G$ 为椭圆曲线上的一个生成元(Generator),$a$ 和 $b$ 为两个整数。我们可以计算出两个点:
$$
\begin{aligned}
A &= aG \\
B &= bG
\end{aligned}
$$
根据椭圆曲线上点的加法规则,我们可以将这两个点相加,得到一个新的点 $D$:
$$
D = A + B = (a+b)G
$$
这里的 $a+b$ 实际上是在有限域上进行模加法运算。
应用
-
多方签名:假设 Alice 和 Bob 分别持有私钥
$a$和$b$,他们可以各自计算出$A=aG$和$B=bG$,然后将这两个公钥相加得到组合公钥$D$。当需要签名时,Alice 和 Bob 分别使用自己的私钥对消息进行签名,然后将两个签名相加,得到最终的组合签名。验证者可以使用组合公钥$D$来验证这个签名的有效性。 -
密钥托管:用户可以将自己的私钥分成两部分
$a$和$b$,分别托管给两个不同的机构。当需要使用私钥时,用户可以从两个机构分别获得$aG$和$bG$,然后自己相加得到完整的公钥$D$。这样可以提高私钥的安全性,防止单点失败。
课程
1. Signatures, Hashing, Hash Chains, e-cash, and Motivation - YouTube
