RNN:原理与实现
RNN基础
什么是RNN
循环神经网络(RNN)是一类用于处理序列数据的神经网络。与传统的前馈神经网络不同,RNN具有“记忆”能力,可以保留和利用之前输入的信息,从而在处理当前输入时,参考上下文环境。
RNN的要点在于通过循环结构传递隐藏状态,使数据在序列中逐步流动并捕捉时间依赖关系。 即:
新隐态 = f(输入, 旧隐态) 输出 = g(新隐态)
RNN 原理:数据流视角
从数据流的视角来看,循环神经网络(RNN)的计算过程可以分为以下几个步骤:
-
输入序列的逐步处理:
- RNN 接收一个输入序列
$x = (x_1, x_2, ..., x_T)$,并在每一个时间步$t$处理对应的输入$x_t$。
- RNN 接收一个输入序列
-
隐藏状态的更新:
-
在每个时间步
$t$,RNN 根据当前输入$x_t$和前一个时间步的隐藏状态$h_{t-1}$,通过以下公式计算当前的隐藏状态$h_t$:$$ h_t = \tanh(W_{xh}x_t + W_{hh}h_{t-1} + b_h) $$-
这里:
-
$W_{xh}$是输入到隐藏层的权重矩阵。 -
$W_{hh}$是隐藏层到隐藏层的权重矩阵。 -
$b_h$是隐藏层的偏置向量。
-
-
作用:隐藏状态
$h_t$既包含了当前时间步的输入信息$x_t$,也保留了前序时间步的上下文信息$h_{t-1}$。
-
-
输出的生成:
-
基于当前的隐藏状态
$h_t$,计算当前时间步的输出$y_t$:$$ y_t = W_{hy}h_t + b_y $$-
这里:
-
$W_{hy}$是隐藏层到输出层的权重矩阵。 -
$b_y$是输出层的偏置向量。
-
-
作用:生成当前时间步的输出结果
$y_t$。
-
-
递归传递与上下文融合:
-
将当前的隐藏状态
$h_t$作为下一个时间步$t+1$的前一隐藏状态$h_{t}$,继续处理后续的输入$x_{t+1}$。 -
通过这种方式,RNN 能够在处理当前输入的同时,结合之前的上下文信息,实现对序列数据的建模。
-
RNN的优势和局限
优势:
-
处理序列数据的能力:RNN能够自然地处理变长的序列输入,不需要固定的输入长度。
-
参数共享:时间步之间参数共享,有助于降低模型复杂度。
局限:
-
梯度消失与梯度爆炸:在长序列中,反向传播时梯度可能会迅速衰减或增大,导致训练困难。
-
长距离依赖问题:传统RNN难以捕捉序列中相隔较远的依赖关系。
RNN 的变种
最具代表性的是长短期记忆网络(LSTM)和门控循环单元(GRU)。但是本文不会细讲。
长短期记忆网络(LSTM)
LSTM 通过引入“细胞状态”和“门控机制”来有效缓解梯度消失问题。其核心组件包括输入门、遗忘门和输出门,控制信息的流动和更新。公式如下:
$$
f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)
$$
$$
i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)
$$
$$
\tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)
$$
$$
C_t = f_t \ast C_{t-1} + i_t \ast \tilde{C}_t
$$
$$
o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)
$$
$$
h_t = o_t \ast \tanh(C_t)
$$
其中,$\sigma$ 表示sigmoid激活函数,$\ast$ 表示按元素相乘。
门控循环单元(GRU)
GRU是LSTM的简化版本,通过合并遗忘门和输入门,减少了参数数量,同时保持了类似的性能。GRU的公式如下:
$$
z_t = \sigma(W_z \cdot [h_{t-1}, x_t] + b_z)
$$
$$
r_t = \sigma(W_r \cdot [h_{t-1}, x_t] + b_r)
$$
$$
\tilde{h}_t = \tanh(W_h \cdot [r_t \ast h_{t-1}, x_t] + b_h)
$$
$$
h_t = (1 - z_t) \ast h_{t-1} + z_t \ast \tilde{h}_t
$$
使用PyTorch实现RNN
项目结构
为使项目结构清晰,我们将代码分离到以下不同的文件中:
rnn_custom_pytorch/
├── data.py # 数据生成与数据集定义
├── model.py # 自定义RNN模型定义
├── train.py # 训练脚本
├── test.py # 测试脚本
├── visualize.py # 结果可视化脚本
├── utils.py # 工具函数(可选)
└── requirements.txt # 依赖包
数据集生成与预处理
data.py
负责生成正弦波数据,并定义PyTorch的数据集和数据加载器。
1import numpy as np
2import torch
3from torch.utils.data import Dataset, DataLoader
4
5# 生成正弦波数据
6def generate_sine_wave(seq_length, num_samples):
7 x = np.linspace(0, num_samples * 0.1, num_samples)
8 y = np.sin(x)
9 data = []
10 for i in range(len(y) - seq_length):
11 data.append(y[i:i+seq_length+1])
12 return np.array(data)
13
14# 自定义数据集
15class SineWaveDataset(Dataset):
16 def __init__(self, data):
17 super(SineWaveDataset, self).__init__()
18 self.x = torch.tensor(data[:, :-1], dtype=torch.float32).unsqueeze(-1) # shape: (batch, seq_len, 1)
19 self.y = torch.tensor(data[:, -1], dtype=torch.float32).unsqueeze(-1) # shape: (batch, 1)
20
21 def __len__(self):
22 return len(self.x)
23
24 def __getitem__(self, idx):
25 return self.x[idx], self.y[idx]
26
27def get_data_loaders(seq_length=50, num_samples=1000, batch_size=32, train_ratio=0.8):
28 data = generate_sine_wave(seq_length, num_samples)
29 train_size = int(train_ratio * len(data))
30 train_data = data[:train_size]
31 test_data = data[train_size:]
32
33 train_dataset = SineWaveDataset(train_data)
34 test_dataset = SineWaveDataset(test_data)
35
36 train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
37 test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
38
39 return train_loader, test_loader
考虑到这个波形太简单,下面是一个替代实现,是多个波的叠加。
1import numpy as np
2import torch
3from torch.utils.data import Dataset, DataLoader
4
5# 生成叠加波形数据
6def generate_combined_wave(seq_length, num_samples):
7 x = np.linspace(0, num_samples * 0.1, num_samples)
8 sine_wave = np.sin(x)
9 cosine_wave = np.cos(x)
10 square_wave = np.sign(np.sin(x))
11
12 # 叠加三种波形
13 combined_wave = sine_wave + cosine_wave + square_wave
14
15 data = []
16 for i in range(len(combined_wave) - seq_length):
17 data.append(combined_wave[i:i+seq_length+1])
18 return np.array(data)
19
20# 自定义数据集
21class CombinedWaveDataset(Dataset):
22 def __init__(self, data):
23 super(CombinedWaveDataset, self).__init__()
24 self.x = torch.tensor(data[:, :-1], dtype=torch.float32).unsqueeze(-1) # shape: (batch, seq_len, 1)
25 self.y = torch.tensor(data[:, -1], dtype=torch.float32).unsqueeze(-1) # shape: (batch, 1)
26
27 def __len__(self):
28 return len(self.x)
29
30 def __getitem__(self, idx):
31 return self.x[idx], self.y[idx]
32
33def get_data_loaders(seq_length=50, num_samples=1000, batch_size=32, train_ratio=0.8):
34 data = generate_combined_wave(seq_length, num_samples)
35 train_size = int(train_ratio * len(data))
36 train_data = data[:train_size]
37 test_data = data[train_size:]
38
39 train_dataset = CombinedWaveDataset(train_data)
40 test_dataset = CombinedWaveDataset(test_data)
41
42 train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
43 test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
44
45 return train_loader, test_loader
46
47# 示例用法
48if __name__ == "__main__":
49 train_loader, test_loader = get_data_loaders()
50 for x, y in train_loader:
51 print(x.shape, y.shape)
52 break
自定义RNN实现
这部分是本文的核心。
model.py
1# model.py
2import torch
3import torch.nn as nn
4import numpy as np
5
6class CustomRNN(nn.Module):
7 def __init__(self, input_size, hidden_size, output_size):
8 super(CustomRNN, self).__init__()
9 self.hidden_size = hidden_size
10 # 输入到隐藏层的权重
11 self.W_ih = nn.Parameter(torch.Tensor(input_size, hidden_size))
12 # 隐藏层到隐藏层的权重
13 self.W_hh = nn.Parameter(torch.Tensor(hidden_size, hidden_size))
14 # 隐藏层到输出的权重
15 self.W_ho = nn.Parameter(torch.Tensor(hidden_size, output_size))
16 # 隐藏层偏置
17 self.bias_h = nn.Parameter(torch.Tensor(hidden_size))
18 # 输出层偏置
19 self.bias_o = nn.Parameter(torch.Tensor(output_size))
20 self.init_parameters()
21
22 def init_parameters(self):
23 # 使用均匀分布初始化权重
24 nn.init.kaiming_uniform_(self.W_ih, a=np.sqrt(5))
25 nn.init.kaiming_uniform_(self.W_hh, a=np.sqrt(5))
26 nn.init.kaiming_uniform_(self.W_ho, a=np.sqrt(5))
27 nn.init.zeros_(self.bias_h)
28 nn.init.zeros_(self.bias_o)
29
30 def forward(self, x):
31 """
32 x: 输入序列,形状为 (batch, seq_len, input_size)
33 """
34 batch_size, seq_len, _ = x.size()
35 h_t = torch.zeros(batch_size, self.hidden_size).to(x.device) # 初始化隐藏状态
36
37 for t in range(seq_len):
38 x_t = x[:, t, :] # 当前时间步输入
39 h_t = torch.tanh(x_t @ self.W_ih + h_t @ self.W_hh + self.bias_h) # 更新隐藏状态
40
41 output = h_t @ self.W_ho + self.bias_o # 最终输出
42 return output
结构如下
### 训练与验证train.py
负责训练模型,并在训练过程中输出损失。
1import torch
2import torch.nn as nn
3import torch.optim as optim
4import time
5from data import get_data_loaders
6from model import CustomRNN
7
8def train_model(
9 input_size=1,
10 hidden_size=32,
11 output_size=1,
12 seq_length=50,
13 num_samples=1000,
14 batch_size=32,
15 train_ratio=0.8,
16 learning_rate=0.01,
17 epochs=100,
18 device=None
19):
20 if device is None:
21 device = 'cuda' if torch.cuda.is_available() else 'cpu'
22
23 # 获取数据加载器
24 train_loader, test_loader = get_data_loaders(
25 seq_length=seq_length,
26 num_samples=num_samples,
27 batch_size=batch_size,
28 train_ratio=train_ratio
29 )
30
31 # 实例化模型
32 model = CustomRNN(input_size, hidden_size, output_size).to(device)
33
34 # 定义损失函数和优化器
35 criterion = nn.MSELoss()
36 optimizer = optim.Adam(model.parameters(), lr=learning_rate)
37
38 # 训练过程
39 for epoch in range(1, epochs + 1):
40 model.train()
41 epoch_loss = 0
42 start_time = time.time()
43 for batch_x, batch_y in train_loader:
44 batch_x = batch_x.to(device)
45 batch_y = batch_y.to(device)
46
47 optimizer.zero_grad()
48 outputs = model(batch_x)
49 loss = criterion(outputs, batch_y)
50 loss.backward()
51 optimizer.step()
52
53 epoch_loss += loss.item() * batch_x.size(0)
54
55 epoch_loss /= len(train_loader.dataset)
56 if epoch % 10 == 0 or epoch == 1:
57 elapsed = time.time() - start_time
58 print(f'Epoch {epoch}/{epochs}, Loss: {epoch_loss:.6f}, Time: {elapsed:.2f}s')
59
60 # 保存模型
61 torch.save(model.state_dict(), 'rnn_custom_model.pth')
62 print('Saved model to rnn_custom_model.pth')
63
64 return model, test_loader
65
66if __name__ == "__main__":
67 train_model()
test.py
加载训练好的模型,并在测试集上评估其性能。
1import torch
2import torch.nn as nn
3from data import get_data_loaders
4from model import CustomRNN
5
6def test_model(model_path='rnn_custom_model.pth',
7 input_size=1,
8 hidden_size=32,
9 output_size=1,
10 seq_length=50,
11 num_samples=1000,
12 batch_size=32,
13 train_ratio=0.8,
14 device=None):
15 if device is None:
16 device = 'cuda' if torch.cuda.is_available() else 'cpu'
17
18 # 获取数据加载器
19 _, test_loader = get_data_loaders(
20 seq_length=seq_length,
21 num_samples=num_samples,
22 batch_size=batch_size,
23 train_ratio=train_ratio
24 )
25
26 # 实例化模型
27 model = CustomRNN(input_size, hidden_size, output_size).to(device)
28 model.load_state_dict(torch.load(model_path, map_location=device))
29 model.eval()
30
31 # 定义损失函数
32 criterion = nn.MSELoss()
33 test_loss = 0
34 with torch.no_grad():
35 for batch_x, batch_y in test_loader:
36 batch_x = batch_x.to(device)
37 batch_y = batch_y.to(device)
38 outputs = model(batch_x)
39 loss = criterion(outputs, batch_y)
40 test_loss += loss.item() * batch_x.size(0)
41
42 test_loss /= len(test_loader.dataset)
43 print(f'Test MSE Loss: {test_loss:.6f}')
44
45 return model, test_loader
46
47if __name__ == "__main__":
48 test_model()
结果与讨论
$ python train.py
Epoch 1/100, Loss: 0.311845, Time: 0.04s
Epoch 10/100, Loss: 0.095100, Time: 0.04s
Epoch 20/100, Loss: 0.071599, Time: 0.04s
Epoch 30/100, Loss: 0.036135, Time: 0.04s
Epoch 40/100, Loss: 0.038392, Time: 0.04s
Epoch 50/100, Loss: 0.028199, Time: 0.04s
Epoch 60/100, Loss: 0.032723, Time: 0.04s
Epoch 70/100, Loss: 0.019848, Time: 0.04s
Epoch 80/100, Loss: 0.026268, Time: 0.04s
Epoch 90/100, Loss: 0.022966, Time: 0.04s
Epoch 100/100, Loss: 0.017622, Time: 0.04s
Saved model to rnn_custom_model.pth
$ python test.py
Test MSE Loss: 0.023389
通过训练和测试脚本,我们可以观察到模型的训练损失逐步下降,测试集上的损失也保持在较低水平,表明模型在学习序列的时间依赖性。为了更直观地理解模型的表现,我们将使用一个单独的脚本进行结果可视化。
visualize.py
选择部分测试样本进行预测,并将预测结果与真实值进行对比。
1import torch
2import numpy as np
3import matplotlib.pyplot as plt
4from data import get_data_loaders
5from model import CustomRNN
6
7def visualize_predictions(
8 model_path='rnn_custom_model.pth',
9 input_size=1,
10 hidden_size=32,
11 output_size=1,
12 seq_length=50,
13 num_samples=256*10,
14 batch_size=256,
15 train_ratio=0.8,
16 device=None,
17 num_plots=100
18):
19 if device is None:
20 device = 'cuda' if torch.cuda.is_available() else 'cpu'
21
22 # 获取数据加载器
23 _, test_loader = get_data_loaders(
24 seq_length=seq_length,
25 num_samples=num_samples,
26 batch_size=batch_size,
27 train_ratio=train_ratio
28 )
29
30 # 实例化模型
31 model = CustomRNN(input_size, hidden_size, output_size).to(device)
32 model.load_state_dict(torch.load(model_path, map_location=device))
33 model.eval()
34
35 # 获取一个批次的数据
36 with torch.no_grad():
37 for batch_x, batch_y in test_loader:
38 sample_x = batch_x.to(device)
39 sample_y = batch_y.to(device)
40 predictions = model(sample_x).cpu().numpy()
41 true = sample_y.cpu().numpy()
42 break # 只取一个批次
43
44 # 绘制部分预测结果
45 plt.figure(figsize=(12,6))
46 plt.plot(true[:num_plots], label='True')
47 plt.plot(predictions[:num_plots], label='Predictions')
48 plt.legend()
49 plt.xlabel('Sample')
50 plt.ylabel('Value')
51 plt.title('Predictions vs True')
52 plt.show()
53 plt.savefig('predictions_vs_true.png')
54
55if __name__ == "__main__":
56 visualize_predictions()
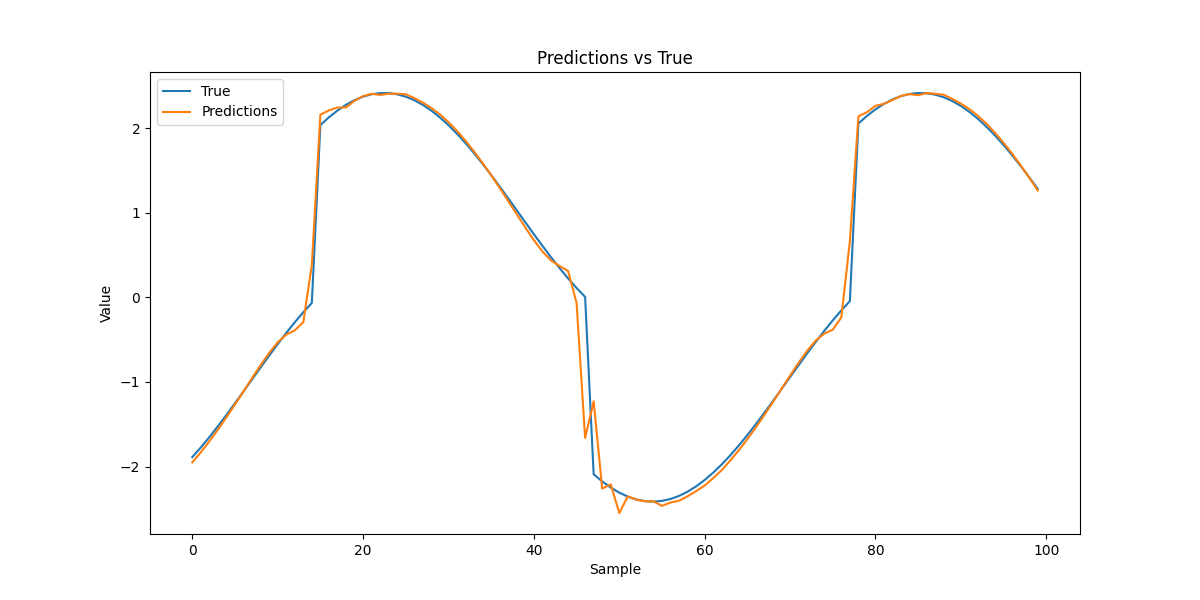
结果如下: