«自动机理论、语言和计算导论»笔记：第六章 下推自动机

下推自动机能够对应 CFG。它是一个带有“栈”的 $\varepsilon-\text{NFA}$ 。

6.1 下推自动机的定义

6.1.1 通俗介绍

下推自动机与 $\varepsilon-\text{NFA}$ 类似，状态控制器可以在有限个状态之间转移（Finite Control）。但是它还有一个符号栈，可以推入（push）写入符号，或者弹出（pop）读取符号。栈的空间可以看作无限的。

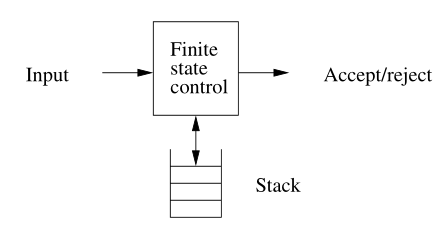
image-20210616221744488

6.1.2 形式定义

PDA 的定义如下：


$$
M = (Q,T,\Gamma , \delta , q_0, z_0, F)
$$

  1. $Q$：有穷状态集。有限控制器的状态集合

  2. $T$：有限输入字母表。

  3. $\Gamma$：有限下推栈字母表。

  4. $\delta$：转移函数。输入：当前状态，当前输入，当前栈顶。输出：新状态，栈顶替换的字符

  5. $q_0$：初态， $q_0 \in Q$

  6. $z_0$：下推栈的栈底最初符号，$z_0 \in \Gamma - T$

  7. $F$：终态集合

如下图，当处于状态 q 时，输入一个字符 $a$ ，则将栈顶 $Z$ 替换为 $\beta_i$ 或者 $\beta _j$

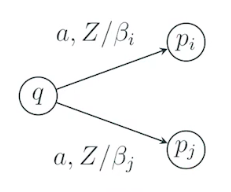
image-20210616223644789

记作：


$$
\begin{array}{l}
\delta(q, a, Z)=\left\{\left(p_{1}, \beta_{1}\right),\left(p_{2}, \beta_{2}\right), \cdots,\left(p_{m}, \beta_{m}\right)\right\}, \quad \text { 或 } \\
\delta(q, \varepsilon, Z)=\left\{\left(p_{1}, \beta_{1}\right),\left(p_{2}, \beta_{2}\right), \cdots,\left(p_{m}, \beta_{m}\right)\right\}
\end{array}
$$

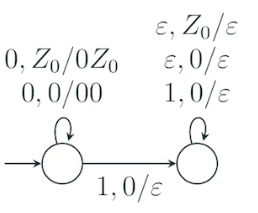
例子：设计 PDA，识别 $L_{01} = \{0^n1^n | n \geq 1\}$

思路：

当 PDA 读入 0 时，压入 0，当读入 1 时，弹出 0. 当字符串读取结束后，到达栈顶，则说明接受字符串。

设起始状态 $q_0$ ，

$q_0 \to q_0$ :

  • $0, 0/00$ (表示输入零，将栈顶的 0 替换为 00，相当于压入 0)

  • $0, Z_0/0Z_0$ (表示输入0，将栈顶的 $Z_0$ 替换为 $0Z_0$，相当于压入 0 )

当输入 1 后到达 $q_1$ :

$q_0 \to q_1$ :

  • $1, 0/\varepsilon$ (表示输入 1, 弹出 0)

$q_1 \to q_1$ :

  • $1, 0/\varepsilon $ (表示输入 1，弹出 0)

为了侦测串结束，只要检查栈顶是 $Z_0$ 即可：

$q_1 \to q_2$ :

  • $\varepsilon , Z_0 / Z_0$

注：00111 不会被接受

6.1.3 瞬时描述

定义元组 $(q,w,\gamma)$ 表示 PDA 处于状态 $q$，输入剩余串 $w$，栈为 $\gamma$，称为瞬时描述（ID，Instantaneous description）。

在 $\text{PDA } P$ 中， $(q, a w, Z \alpha)$ 到 $(p, w, \beta \alpha)$ 的变化, 称为 ID 的转移 $\vdash_{P}$, 记为


$$
(q, a w, Z \alpha) \vdash_{P}(p, w, \beta \alpha)
$$

$\vdash_{P}^{*}$ 表示 ID 的 0 次或多次转移。

6.2 PDA 接受的语言

6.2.1 PDA 的接受方式

PDA $P$ 以终态方式接受的语言，记为 $\mathrm{L}(P)$, 定义为


$$
\mathrm{L}(P)=\left\{w \mid\left(q_{0}, w, Z_{0}\right) \vdash^{*}(p, \varepsilon, \gamma), p \in F\right\}
$$

$P$ 以空栈方式接受的语言，记为 $\mathrm{N}(P)$, 定义为


$$
\mathbf{N}(P)=\left\{w \mid\left(q_{0}, w, Z_{0}\right) \vdash^{*}(p, \varepsilon, \varepsilon)\right\}
$$

终态方式接收，就是空转移到终态（$\varepsilon , Z_0 / Z_0$），即用明确的状态表示中止。

空栈方式接收，就是接收字符串时弹空（$Z_0/\varepsilon$），导致栈空，表明接受。可以在任何状态中止。

定理：若 PDA $P_F$ 以终态接受语言，则一定存在 PDA $P_N$ 以空栈方式接受同语言。

证明略。思路为用 $P_N$ 模拟 $P_F$

6.3 PDA 与 CFG 的等价性

6.3.1 文法转 PDA

PDA 的特点是弹出一个符号，压入一个串。因此可用此过程模拟 CFG 的最左推导。

例子：设计 $L = \{0^n 1^m | a \leq m \leq n\}$ 的 PDA

解：

要接受的字符串的特点是：0 多余 1

image-20210616235058191

PDA 如上图。功能：

  1. 输入 0，则压入

  2. 一旦输入了 1，则弹出 0. 1 可以和 0 成对弹出，也可以空转弹出，从而保证 0 的数量大于等于 1 的数量。扫描完露出栈顶。

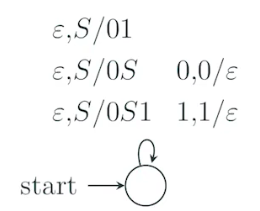
image-20210616235514185

如上图，我们将 S 作为栈底符号。通过非确定方式在栈中产生足够的 01 串（0S1, 0S, 01）（类似穷举出所有可能）,当栈顶是 0 或 1 时，不断匹配出栈。只要输入串和穷举中任何一个相同就引发接受。

其对应的文法：


$$
S \to 0S1 | 0S | 01
$$

就类似最左派生。

定理： $\forall \text{ CFL } L, \exists \text{ PDA } P \text{ s.t. } L = \mathrm{N}(P)$

【例子】 为 $S\to aAA, A \to aS | bS | a$ 构造 PDA.

【分析与解答】

单状态 $q_0 \to q_0$ :

  • $\varepsilon , s/aAA$

  • $\varepsilon , A/aS$

  • $\varepsilon , A/bS$

  • $\varepsilon , A/a$

  • $a,a / \varepsilon $

  • $b,b / \varepsilon $

6.3.2 GNF 转 PDA

如果 $\mathrm{GNF}$ 格式的 $\mathrm{CFG} G=\left(V, T, P^{\prime}, S\right)$, 那么构造 $\mathrm{PDA}$


$$
P=(\{q\}, T, V, \delta, q, S, \varnothing)
$$

构造特点：

只有一个状态 $q$ 并且是开始状态 输入符号表 T 刚好是终结符 栈符号表 V 刚好是非终结符 栈底符号刚好是开始符号 不需要终态，因为以空栈接受

为每个产生式, 定义 $\delta$ 为:


$$
\delta(q, a, A)=\left\{(q, \beta) \mid A \rightarrow a \beta \in P^{\prime}\right\}
$$

产生式定义为终结符( $a$ )连接变元符号串( $\beta$ )

【例子】 为 GNF 文法 $S\to aAA, A \to aS | bS | a$ 构造 PDA.

【分析与解答】

单状态 $q_0 \to q_0$ :

  • $a,S/AA$

  • $a,A/S$

  • $b,A/S$

  • $a,A/\varepsilon $

6.3.3 PDA 转 CFG

定理：若 PDA P, $L = \mathrm{N}(P)$ 则 L 是 CFG.

【例子】 将 $\text{PDA } P = (\{p, q\}, (0,1), \{X,Z\}, \delta, q, Z)$ 转为 CFG. $\delta $ 定义如下：

(1) $\delta(q, 1, Z)=\{(q, X Z)\}$ (2) $\delta(q, 1, X)=\{(q, X X)\}$ (3) $\delta(q, 0, X)=\{(p, X)\}$ (4) $\delta(q, \varepsilon, Z)=\{(q, \varepsilon)\}$ (5) $\delta(p, 1, X)=\{(p, \varepsilon)\}$ (6) $\delta(p, 0, Z)=\{(q, Z)\}$

https://www.bilibili.com/video/BV1oE4116794?p=31&spm_id_from=pageDriver


$$
\begin{array}{l}
\begin{array}{l|l}
\hline \delta & \text { 产生式 } \\
\hline \text { (0) } & S \rightarrow[q Z q] \\
& S \rightarrow[q Z p] \\
\text { (1) } & {[q Z q] \rightarrow 1\left[q X_{0} q\right][q Z q]} \\
& {[q Z q] \rightarrow 1[q X p][p Z q]} \\
& {[q Z p] \rightarrow 1[q X q][q Z p]} \\
& {[q Z p] \rightarrow 1[q X p][p Z p]} \\
\text { (2) } & {[q X q] \rightarrow 1[q X q][q X q]} \\
& {[q X q] \rightarrow 1[q X p][p X q]} \\
& {[q X p] \rightarrow 1[q X q][q X p]} \\
& {[q X p] \rightarrow 1[q X p][p X p]} \\
\text { (3) } & {[q X q] \rightarrow 0[p X q]} \\
& {[q X p] \rightarrow 0[p X p]} \\
\text { (4) } & {[q Z q] \rightarrow \varepsilon} \\
\text { (5) } & {[p X p] \rightarrow 1} \\
\text { (6) } & {[p Z p] \rightarrow 0[q Z p]} \\
& {[p Z q] \rightarrow 0[q Z q]} \\
\hline
\end{array}\\
\end{array}
$$


$$
\begin{array}{l}
\hline \text { 消除无用符号 } \\
\hline S \rightarrow[q Z q] \\
{[q Z q] \rightarrow 1[q X p][p Z q]} \\
{[q X p] \rightarrow 1[q X p][p X p]} \\
{[q X p] \rightarrow 0[p X p]} \\
{[q Z q] \rightarrow \varepsilon} \\
{[p X p] \rightarrow 1} \\
{[p Z q] \rightarrow 0[q Z q]} \\
\hline
\end{array}
$$

过程详解：

$S\to[qZ?]$

展开：

  • $S\to[qZp]$

  • $S\to[qZq]$

S 定义为所有的开始状态（ $q_0,z_0, p$ ）, $q_0 = q, z_0 = Z$ ， $p = p | q$

对于 $\delta (q, 1, Z) = \{(q, XZ)\}$

从状态 q, 为了弹出 Z，可能到达任意状态。消耗 1，Z 替换成 [ X ][ Z ].

消耗 1，到达 q：$[qZ?]\to 1[qX?][?Z?]$

展开就是：


$$
 \left\{\begin{array}{cc}
& {[q Z q] \rightarrow 1\left[q X_{0} q\right][q Z q]} \\
& {[q Z q] \rightarrow 1[q X p][p Z q]} \\
& {[q Z p] \rightarrow 1[q X q][q Z p]} \\
& {[q Z p] \rightarrow 1[q X p][p Z p]} \\
\end{array}\right.
$$

确定型下推自动机（DPDA）

如果对于每个输入，后续状态唯一，则为 DPDA。

最近发布

要查看全部文章，请点击右上角“归档”

随机文章