«自动机理论、语言和计算导论»笔记：第五章 上下文无关文法与语言

5.1 上下文无关文法

5.1.1 回文语言

回文串就是正反一样的串，比如 abccba，010。我们无法用有限自动机、规则式来表达这种文法，但用生成式可以：

1. $P \to \varepsilon $

2. $P \to 0$

3. $P \to 1$

4. $P \to 0P0$

5. $P \to 1P1$

1~3 表明：回文串的构成包括： $\varepsilon $, $0$, $1$

4~5 规定了回文串的生成规则

回文语言是一种典型的上下文无关语言。

5.1.2 上下文无关文法（CFG）的定义

定义：

1. $T$ ：终结符（terminals）

2. $N$，or $V$ ：变量（variables），也称非终结符（nonterminals）

3. $S$ ：开始符号

4. $P$ ：产生式（productions），又叫规则（rules）

5.1.3 使用文法的推导

推导就是代入生成式的过程。

5.1.4 最左和最右推导

代入时总是替换最左边的变量，是最左推导（Leftmost derivation）。同理有最右推导

5.1.5 文法的语言

就是 CFG 所能推导出的所有终结串的集合。

5.1.6 句型

初始符号推出来的（不一定终结的）串，叫做句型（Sentential Forms）。通过最左推导产生的句型，是最左句型。同理有 最右句型。

5.2 语法分析树（Parse Tree）

语法分析树是推导的一种表示法。下图是 a*(a+b00) 的分析树：

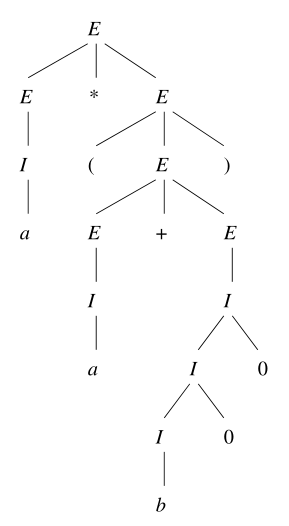
5.3 文法与语言的歧义

5.3.1 歧义文法

若文法有两种推导，推出同一个句型，则称文法有歧义。

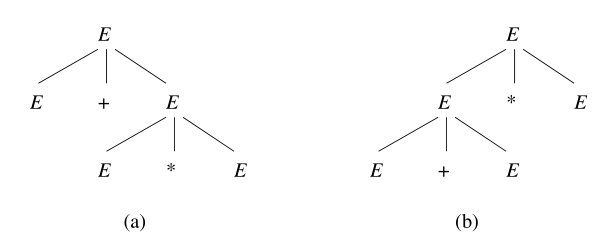
5.3.2 消歧义

CFG 的歧义性不可判定。同时，有的语言只存在歧义文法，不存在无歧义文法（固有歧义）。对于可消歧义的文法，常用的消歧义方法有：

1. 设定优先级（precedence）。

2. 设定默认结合（group）方式。

5.4 CFG 的简化

无用符号的删除及相关算法。

如果符号 X 能够存在于 $S \stackrel{*}{\Rightarrow} w$ 中，即存在 $\mathbf{S} \stackrel{*}{\Rightarrow} \alpha \boldsymbol{X} \boldsymbol{\beta} \stackrel{*}{\Rightarrow} \boldsymbol{w}$，则 X 是有用符号。否则是无用符号。

其实就是存在一个句子能够表明它的推导过程中 X 用得着，那么 X 就是有用符号。

CNF 范式

CNF 的定义

若 2 型文法 $G = (N,T,P,S)$ 生成式形式都是 $A \to a $ 和 $A \to BC$ , 其中 $ A,B,C \in N, a \in T$ 且 $G$，则 $G$ 称为 Chomsky 范式（GNF）

定理：任何 2 型文法都具有等效的 CNF

GNF 范式

GNF 的定义

若 2 型文法 $G = (N,T,P,S)$ 生成式形式都是 $A \to a \beta $ , 其中 $ A \in N, a \in T, \beta \in N^*$ 且 $G$ 不含 $\varepsilon $ 生成式，则 $G$ 称为 Greibach 范式（GNF）

定理：任何 2 型文法都具有等效的 GNF