«自动机理论、语言和计算导论»笔记:第四章 规则式的性质
4.1 泵引理
泵引理(pumping lemma)用于证明语言不是规则语言。它是一个重复不必要条件。
定理:$L$ 是规则语言。则存在 $n$ 满足:只要字符串 $w$ 的长度 $|w|\geq n$,就能将 $w$ 分为三段,$w = xyz$,使得:
-
$y \ne \varepsilon$ -
$|xy|\leq n$ -
对任意
$k \geq 0$,$xy^k z$属于$L$
我们可以通俗地理解:规则语言只能存放有限个状态,所以只要一个字符串足够长,肯定要耗尽所有状态,折回去使用已经用过的状态,从而,字符串的中间 $y$ 必可重复。
4.2 规则语言的封闭性
如果两个语言是规则的,则对二者执行特定运算之后得到的语言同样是规则的。
这些运算包括:
-
交并补差
-
反转、闭包(*)、连接
-
同态和逆同态
4.3 规则语言的判定性质
4.4 自动机的等价性和最小化
对于状态 $p,q$,如果对于任意输入串 $w$,$\hat{\delta}(p,w)$ 是接受状态和 $\hat{\delta}(q,w)$ 二者互为充要条件,说明 $p,q$ 状态等价。否则说 $p,q$ 状态可区分。
就是说,如果
$p,q$对于任意输入表现的行为完全一致(要么最终都接受,要么最终都不接受),那么$p,q$等价。
4.4.1 填表算法
这是一种常见的递归算法,用于寻找 DFA 的可区分状态对。
例子:
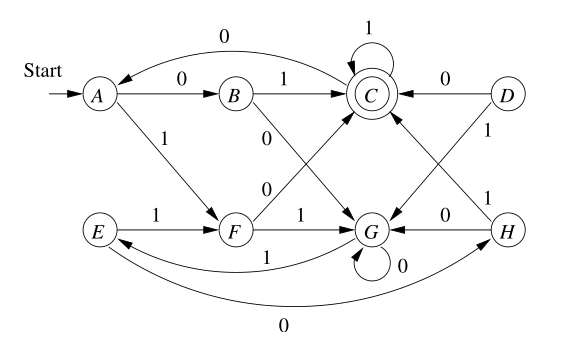
有八个状态,可以形成 $7\times 8=56$ 个状态对。所以列表如下:
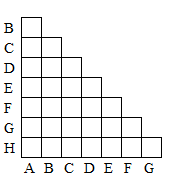
由于 C 是唯一的接受状态,所以涉及 C 的状态是可区分的:
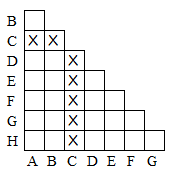
假定输入串结尾是 0,则只能从 F,D 到达 C,所以 F,D 各自与其它状态都是可区分的:
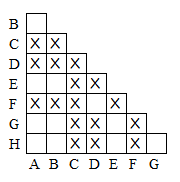
假定输入串结尾是 1,则只能从 B,H,C 到达 C,所以 B,H 各自与其它状态都是可区分的:
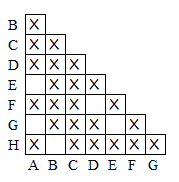
对 A,G 输入 1,分别到达 E,F。由于 E,F 是可区分的,所以 A,G 输入 1 到达了不同状态,因此 A,G 也是可区分的。同理 E,G 也是可区分的:
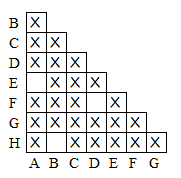
此时剩下的都是不可区分的状态对。
4.4.2 DFA 最小化
将等价的状态合并,即可完成最小化。
