«自动机理论、语言和计算导论»笔记:第三章 规则式与规则语言
3.1 规则式
规则式(RE,RegEx,Regular Expression,正则表达式)用于描述字符串的字符组织规则(也即语言)。例如 :01*+10*,表示 0 开头,后面跟着任意个1;或者 1 开头,后面跟着任意多个 0.
如果有语言 L, M。则语言的并就是二者所能表示的串的集合的并。语言的连接是二者所能表示的串的连接的集合(“笛卡尔”连接,意会一下)。语言的闭包:语言自己和自己的任意次连接的集合。
例如 $L = \{0, 1\}$,则 L 的闭包 $L* = \{0,1\}*$ 是所有 0,1 构成的串,0, 00, 000, ..., 01, 10, 11, 100, 101 ...。
例如,所有 01 交替的串的规则式:
$$
(01)* + (10)* + 0(10)* + 1(01)*\\
= (\varepsilon +1)(01)*(\varepsilon +0)
$$
3.2 DFA 和 RE
任何 DFA 都可以写成 RE
3.2.1 DFA 转 RE
例子:这个 DFA $A$,接受所有至少一个 0 的串。
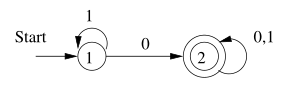
假设状态 i 到 j 之间的路径可以用串 w 表示,串 w 的 RE 记作 $R_{ij}^(k)$,路径上没有大于 $k$ 的中间状态。
我们可以穷举出:
-
$R_{11}^{(0)} = \varepsilon + 1$ -
$R_{12}^{(0)} = 0$ -
$R_{21}^{(0)} = \varnothing $ -
$R_{22}^{(0)} = (\varepsilon + 0 + 1)$
根据定理:
$$
R_{ij}^{(k)} = R_{ij}^{(k-1)} + R_{ik}^{(k-1)} (R_{kk}^{(k-1)})^* R_{kj}^{(k-1)}
$$
代入得:
-
$R_{11}^{(1)} = 1^*$ -
$R_{12}^{(1)} = 1^*0$ -
$R_{21}^{(1)} = \varnothing $ -
$R_{22}^{(1)} = (\varepsilon + 0 + 1)$
同理的继续迭代得到:
-
$R_{11}^{(2)} = 1*$ -
$R_{12}^{(2)} = 1^*0(0+1)^*$ -
$R_{21}^{(2)} = \varnothing $ -
$R_{22}^{(2)} = (0 + 1)^*$
由于 1 是初始状态,2 是接受状态,取 $R_{12}^{(2)}$ 作为最终结果:
$$
1*0(0+1)*
$$
3.2.2 状态消除法
3.2.1 的方法,对于一个 n 状态自动机要构造 $n^3$ 个表达式,代价较高。使用状态消除法,将中间状态替换为一个等效的正则表达式,重复此过程,即可完成转换。详见此文。
3.2.3 RE 转 NFA
定理:所有 RE 定义的语言都可以由 FA 定义。
对于 $r+s$ 型,可以构造为:
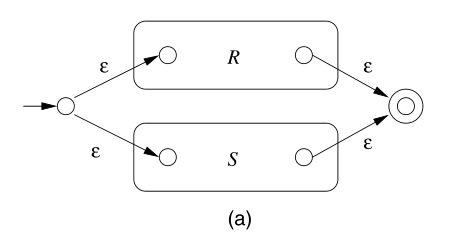
对于 $rs$ 型,可以构造为:
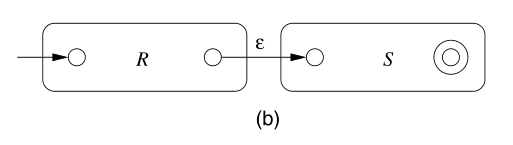
对于 $r*$ 型,可以构造为:
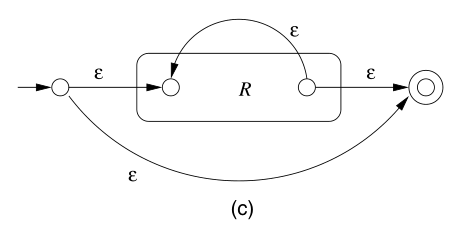
例子:将 $(0+1)*1(0+1)$ 构造为 $\varepsilon-\text{NFA}$
分解,构造 $a*1a$ 的自动机即可,其中 $a = 0+1$
3.3 RE 的代数法则
3.3.1 基本规则
并运算($+$)满足:
-
可结合
-
可交换
-
幂等
-
幺元为
$\varnothing$
连接运算($\cdot$)满足:
-
可结合
-
零元为
$\varnothing$ -
幺元为
$\varepsilon$
连接运算不可交换。
并运算和连接运算可分配。
闭包运算:
-
$(L^*)^* = L^*$ -
$\varnothing^* = \varepsilon$ -
$\varepsilon^* = \varepsilon$ -
$L^* = L^++\varepsilon$ -
$(\varepsilon+L)^* = L^*$
如果两个 RE 表达相同的语言,那么两个规则式等价。例如:
$$
(a+b)^*=(a^*b^*)^*
$$
3.3.2 R 规则
R 规则:R = aR + b <=> a*b
$$
\begin{align}
R&=aR+b\\
&=a(aR+b)+b\\
&=a^2R + ab + b\\
&=a^2(aR+b) + ab + b\\
&=a^3 R + a^2b + ab + b\\
&\quad\cdots\\
&=(a^n + a^{n-1} + \cdots + a^2 + a + \varepsilon )b\\
&=a^*b
\end{align}
$$
