«自动机理论、语言和计算导论»笔记：第二章 有限自动机

2.1 确定有限自动机（Deterministic Finite Automata）

2.1.1 定义

一个 DFA 可以如此描述：

1. 一个状态集合 $Q$

2. 一个输入符号集合 $T$

3. 一个转移函数 $d$。这个函数接受一个输入字符，返回一个新的状态。

4. 一个初始状态 $q_0$

5. 一个终末状态集合 $F$

下面 $q_F$ 表示 $F$ 中的元素。

2.1.2 处理串

如果一个输入序列（输入串）能够使得 DFA 从 $q_0$ 经过一系列状态转移到 $q_F$ ，则称 DFA 接受（Accept）此串。因此 $F$ 也称为接受状态。

DFA 所接受的所有串的集合称作 DFA的语言。

NFA 同理

2.1.3 DFA 的简记法

状态转移图：

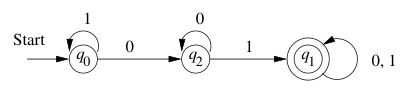
状态转移表：

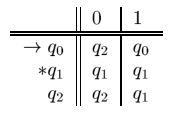
$\rightarrow $ 表示初始状态。 $*$ 表示终末状态。

2.1.4 扩展转移函数（Extended T ransition F unction）

扩展转移函数把输入扩展到一个串，其实就是对各个输入，依次串行调用（依次在状态间跳转），返回值为 处理完这个串后到达的状态。

2.2 非确定有限自动机（Nondeterministic Finite Automata）

NFA 能够同时处在几个状态。因此若是识别同样的语言，NFA 能够更加简练。

试看下面的 NFA：

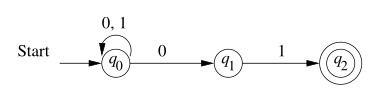
对于 00101 输入，会产生不同的分支。例如输入 0 后，同时进入了 $q_0$ 和 $q_1$ 状态……最后，只要有一条路径能够通向 $q_F$，就认为此串被 NFA 接受了。

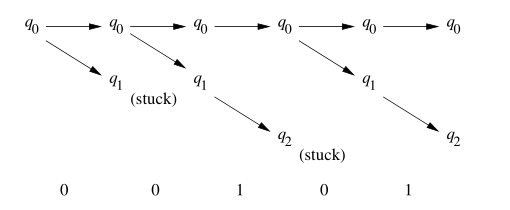
2.2.1 定义

NFA 的定义和 DFA 的唯一区别在于，NFA 返回一个状态的集合。

2.2.2 扩展转移函数

NFA 的扩展转移函数，返回的是状态机处理字符串 w 后处在的各状态（构成的集合）。

2.2.5 NFA 和 DFA 是等价的

任意用 NFA 描述的语言也能用某个 DFA 来描述，反之亦然。

子集构造法（important!）可以实现从 NFA 到 DFA 的转换。

2.3 带 $\varepsilon $ 转移的 FA

带 $\varepsilon $ 转移的意思是，即使不进行任何输入（空输入）也要发生转移。

例如下面是识别 web 或 ebay 两个串的 NFA：

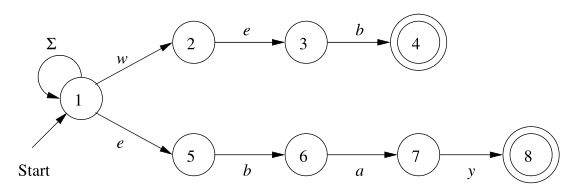
而改成 $\varepsilon-\text{NFA}$ 之后是这样的：

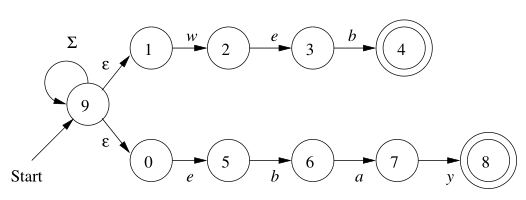
2.3.1 $\varepsilon-\text{NFA}$ 的定义

NFA 和 $\varepsilon-\text{NFA}$ 的唯一区别在于，转移函数必须至少有一个是无条件（空输入）转移的。

2.3.2 Epsilon-闭包

通俗来讲就是，对于一个状态 q，顺着从 q 出发的所有 $\varepsilon $ 转移能够达到的状态，以及重复这一过程能够到达的所有状态，组成了 ECLOSE(q). 说白了，就是空转移所达各状态。

2.3.3 消除空转移

important!