如何直观理解正规子群？

如果学群论前学过线性代数，应该能一眼盯真（

定义。 设 $H$ 是群 $G$ 的一个子群，若对于 $G$ 中的任意元素 $g$，都有 $gHg^{-1} = H$，即 $\forall g \in G, \ gH g^{-1} = H$，则称 $H$ 是 $G$ 的一个正规子群（Normal Subgroup），记作 $H \trianglelefteq G$。

在群论中，两个群元素 $a$ 和 $b$ 被称为共轭的，如果存在一个群元素 $g$ 使得

$$
b = g a g^{-1}
$$

扩展到群，如果满足：$gHg^{-1} \subseteq H \quad \forall g \in G$

这就是正规子群的定义。

即：如果整个子群每个元素共轭后仍然属于这个子群，那么这个子群是正规的。

所以只要你理解共轭，你就理解正规子群。

相信学过线代的大学牲们已经反应过来了。两个矩阵 $A$ 和 $B$ 被称为相似的，如果存在一个可逆矩阵 $P$ 使得

$$
B = P A P^{-1}
$$

相似的两个矩阵特征值、秩等都是一样的。这其实就是共轭。矩阵相似保持线性算子的结构特性不变。同样的，正规子群 $H$ 的定义确保了 $H$ 对群 $G$ 的共轭操作是封闭的，保持了子群的结构不变。

因此，从直观上看，正规子群 $H$ 是群 $G$ 中一个在「内部结构上对称且稳定」的部分。无论我们如何通过群 $G$ 的元素对 $H$ 进行「旋转」或「翻转」（即共轭操作），$H$ 都不会改变其自身的结构和性质。

例子：考虑实数的加法群 $(\mathbb{R}, +)$ 和其子群 $H = \mathbb{Z}$（整数集合）。对于任意 $g \in \mathbb{R}$，有：

$$
g + \mathbb{Z} - g = \mathbb{Z}
$$

这表明 $\mathbb{Z}$ 是 $\mathbb{R}$ 的正规子群。从结构观点，表明对整数在数轴上平移，然后移回，整数自身不变。

反例：考虑对称群 $S_3$（所有排列的群）和其子群 $H = \{ e, (1\,2) \}$。取 $g = (1\,3)$，则：

$$
gHg^{-1} = \{ e, (1\,3)(1\,2)(1\,3)^{-1} \} = \{ e, (2\,3) \} \neq H
$$

因此，$H$ 不是 $S_3$ 的正规子群。

从结构观点，也可以直观理解，对于 $(1,2)$，先进行 $(1,3)$ 置换，再进行 $(1,2)$ 置换，最后 $(3,1)$ 无法换回 $(1,2)$。或者简言之涉及了翻转，翻转之后再进行别的变换，然后翻转回来，不保证和原来的操作效果一样。

例子： $S_3$ 的 3-周期置换：$(123)$、$(132)$ 并上单位元，是一个正规子群。直观上理解可以看作是三角形的旋转对称。它们将三角形顺时针或逆时针旋转 120 度。这是因为你旋转之后，再进行别的变换比如翻转，再旋转回来，可以保证和仅翻转一样。

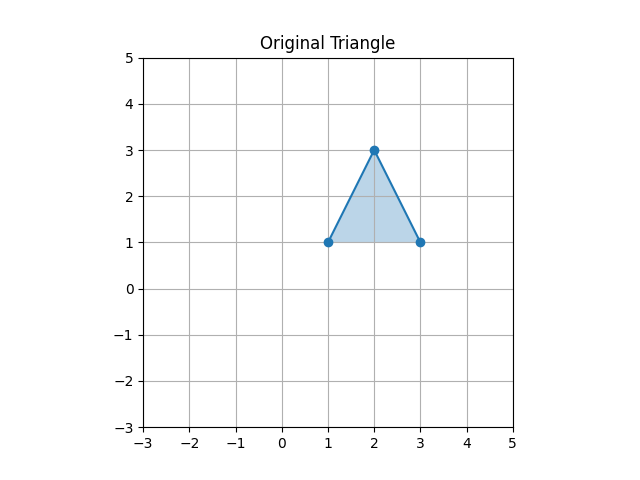
再来个可视化的例子：

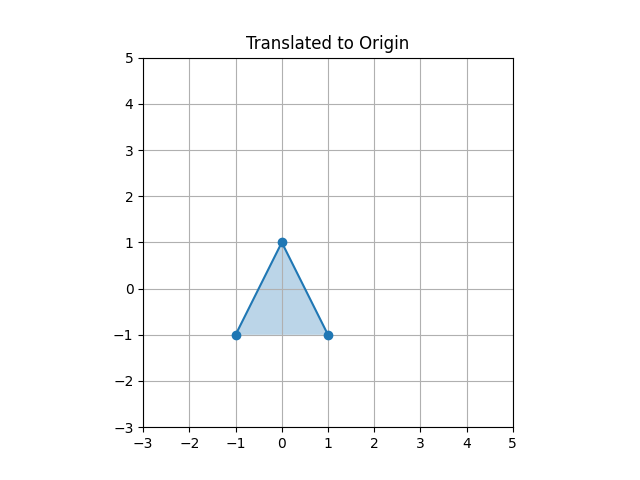
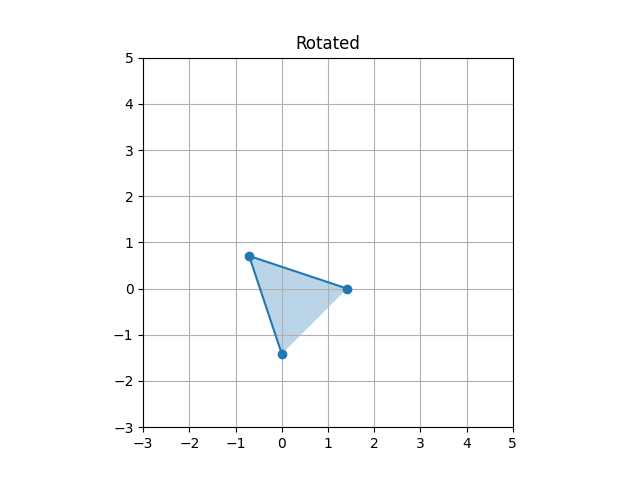
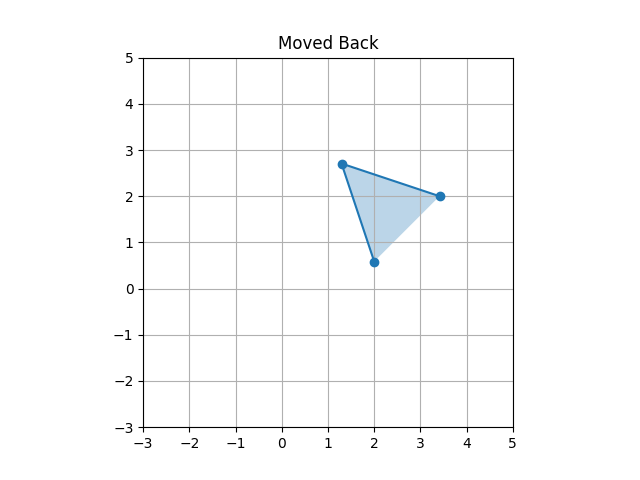
示范对三角形的旋转，这个三角形不在原点。共轭操作的直观原理是将三角形平移到参考点（原点）然后施加旋转，然后再平移回原位置。（学图形学的同学是不是感到眼熟了）

仿射变换在平面上形成一个群，通常表示为 $\text{Aff}(2)$，其元素可以表示为：

$$
\begin{bmatrix}
A & \mathbf{b} \\
\mathbf{0}^T & 1
\end{bmatrix}
$$

其中 $A$ 是线性变换（如旋转、缩放等），而 $\mathbf{b}$ 是平移向量。

所有仅包括平移的仿射变换构成一个子群 $T \subseteq \text{Aff}(2)$。这个子群是 正规子群，因为对于任意的仿射变换 $g \in \text{Aff}(2)$，有：

$$
gTg^{-1} \subseteq T
$$

这意味着平移子群在仿射变换群中是封闭且不变的。

附上代码：

 1import numpy as np
 2import matplotlib.pyplot as plt
 3
 4triangle = np.array([[1, 1], [2, 3], [3, 1]])
 5
 6triangle_homogeneous = np.hstack((triangle, np.ones((triangle.shape[0], 1))))
 7
 8tx, ty = -2, -2
 9
10T = np.array([
11    [1, 0, tx],
12    [0, 1, ty],
13    [0, 0, 1]
14])
15
16T_inv = np.array([
17    [1, 0, -tx],
18    [0, 1, -ty],
19    [0, 0, 1]
20])
21
22theta = np.radians(45)
23
24R = np.array([
25    [np.cos(theta), -np.sin(theta), 0],
26    [np.sin(theta), np.cos(theta), 0],
27    [0, 0, 1]
28])
29
30def plot_triangle(triangle, title, filename):
31    plt.figure()
32    plt.plot(*triangle.T, 'o-', label='Triangle')
33    plt.fill(*triangle.T, alpha=0.3)
34    plt.xlim(-3, 5)
35    plt.ylim(-3, 5)
36    plt.gca().set_aspect('equal', adjustable='box')
37    plt.title(title)
38    plt.grid(True)
39    plt.savefig(filename)
40    plt.close()
41
42triangle_translated = (T @ triangle_homogeneous.T).T
43plot_triangle(triangle_translated[:, :2], 'Translated to Origin', 'step2_translated.png')
44
45triangle_rotated = (R @ triangle_translated.T).T
46plot_triangle(triangle_rotated[:, :2], 'Rotated', 'step3_rotated.png')
47
48triangle_final = (T_inv @ triangle_rotated.T).T
49plot_triangle(triangle_final[:, :2], 'Moved Back', 'step4_final.png')
50
51plot_triangle(triangle, 'Original Triangle', 'step1_original.png')