如何直观地理解同态和同构？

本文图文并茂，欢迎知友食用，包教包会。

---

其实直接结合定义就可以直观理解。

同态

同态是保持代数结构的映射。在群论中，设 $(G, \cdot)$ 和 $(H, *)$ 为两个群，映射 $\phi: G \to H$ 如果满足对于所有 $a, b \in G$：

$$
\phi(a \cdot b) = \phi(a) * \phi(b)
$$

则称 $\phi$ 是一个群同态。

同构

同构是一个特殊的同态，表示两个群在代数结构上是等价的。具体来说，设 $(G, \cdot)$ 和 $(H, *)$ 是两个群。如果存在一个双射（双向一一对应）的群同态 $\phi: G \to H$，则称 $\phi$ 是一个群同构。

理解同态

首先，理解同态定义的重点是映射和运算的顺序顺序无关性。

• 定义的右侧表示先映射后运算：

  • $a,b$ 映射后是 $\phi(a), \phi(b)$，运算结果是 $\phi(a) * \phi(b)$

• 左侧是先运算后映射：

  • $a,b$ 在原集合运算后是 $ab$，$ab$ 映射后是 $\phi(ab)$

• 也就是说，先运算后映射，和先映射后运算，结果是一样的，这种性质被定义为同态。

这个定义导致同态的映射是有损的。主要是两点：

1. 信息丢失：同态映射不一定是双射（双射即一一对应）。因此，多个不同的元素在映射后可能对应到相同的元素（实际被核捕获了），这意味着映射过程中可能丢失信息。

2. 不一定可逆：由于同态映射可能不是双射，因此无法保证存在逆映射将结果唯一地映射回原来的元素。这进一步说明映射可能是有损的。

从而引出核、像的概念。

核测量了映射的有损程度。

• 核包含了所有在同态 $\phi$ 下被“压缩”到 $H$ 的单位元的元素。它描述了同态的“失去”的信息。

• 比如在线性代数中，核是所有被线性变换映射到零向量的向量的集合。

像的大小决定了映射的覆盖范围。

• 像是 $\phi$ 可以“覆盖”到的 $H$ 中的元素。表示了同态的“输出空间”。

• 比如在线性代数中，像是所有可以通过线性变换得到的向量的集合。

理解同构

理解同构定义的重点是映射的一一性。一一性意味着：

1. 核只有单位元，同态是单射（不同元素映射到不同的结果）。

   1. 具体来说，意味着只有 $g = e_G$ 能映射到 $e_H$。假设 $a,b$ 映射到相同的结果，即 $\phi(a) = \phi(b)$，则 $\phi(ab^{-1}) = e_H$，意味着 $ab^{-1} \in \ker(\phi)$。核只有单位元，$ab^{-1} = e_G$，所以 $a = b$。说明能映射到相同结果的不能是不同的元素。

2. 像覆盖目标集合，同态是满射（每个目标元素都有原集合中的元素映射到它）。

这样我们就证明了两个的运算结构完全相同，元素完全一一对应，性质上也完全等价，所以直观点就是“在代数结构上完全等价”，更进一步就是 可互换性 任何在一个群中可以进行的代数操作和推理，都可以在另一个群中进行。

我们之间结合一个具体例子理解。考虑整数加法群 $(\mathbb{Z}_4, +)$ 和四元旋转群 $(C_4, \cdot)$，它们是同构的。当然，乍一看好像只有元素数量一样：

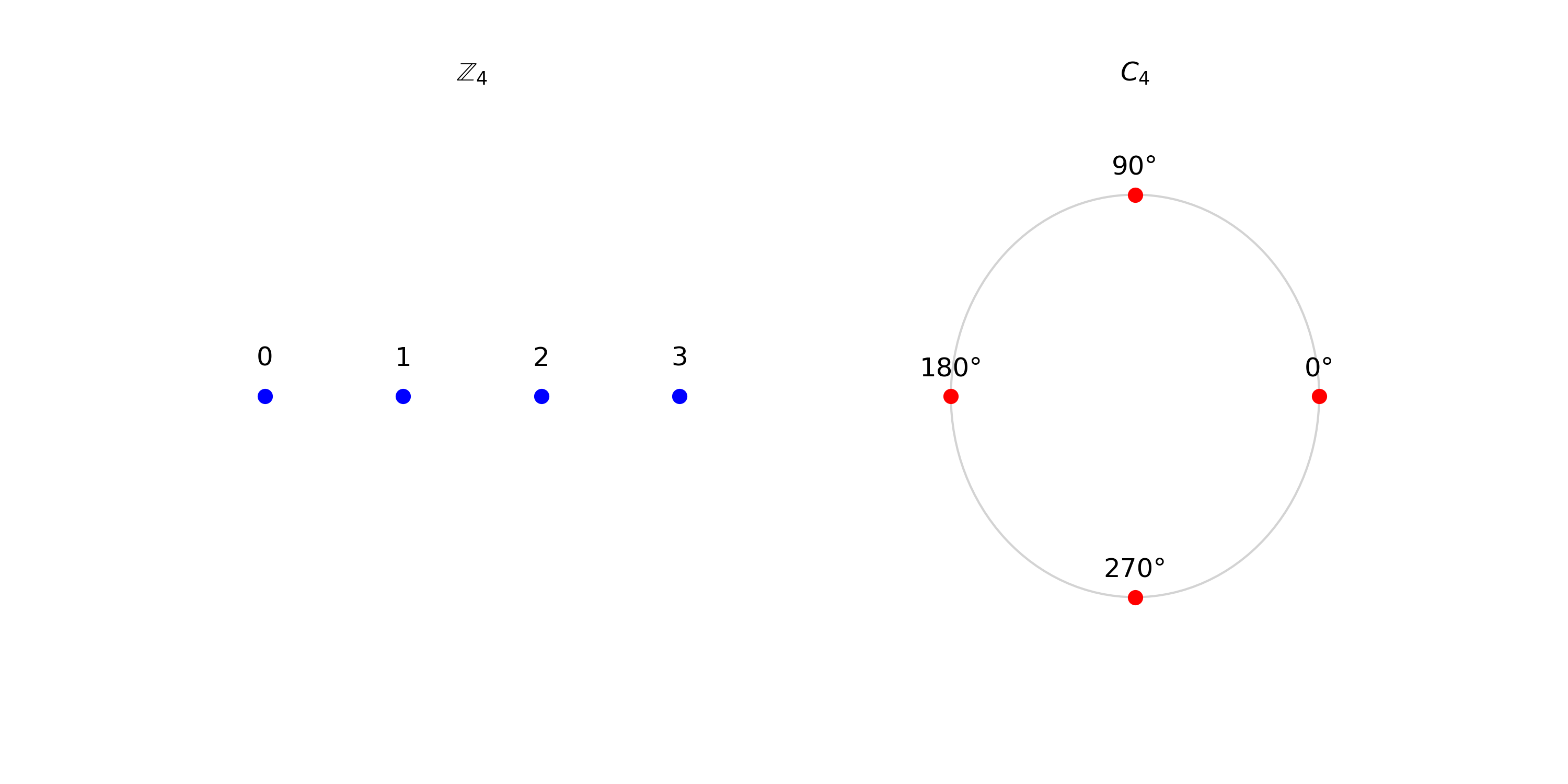
但是我们换种画法：

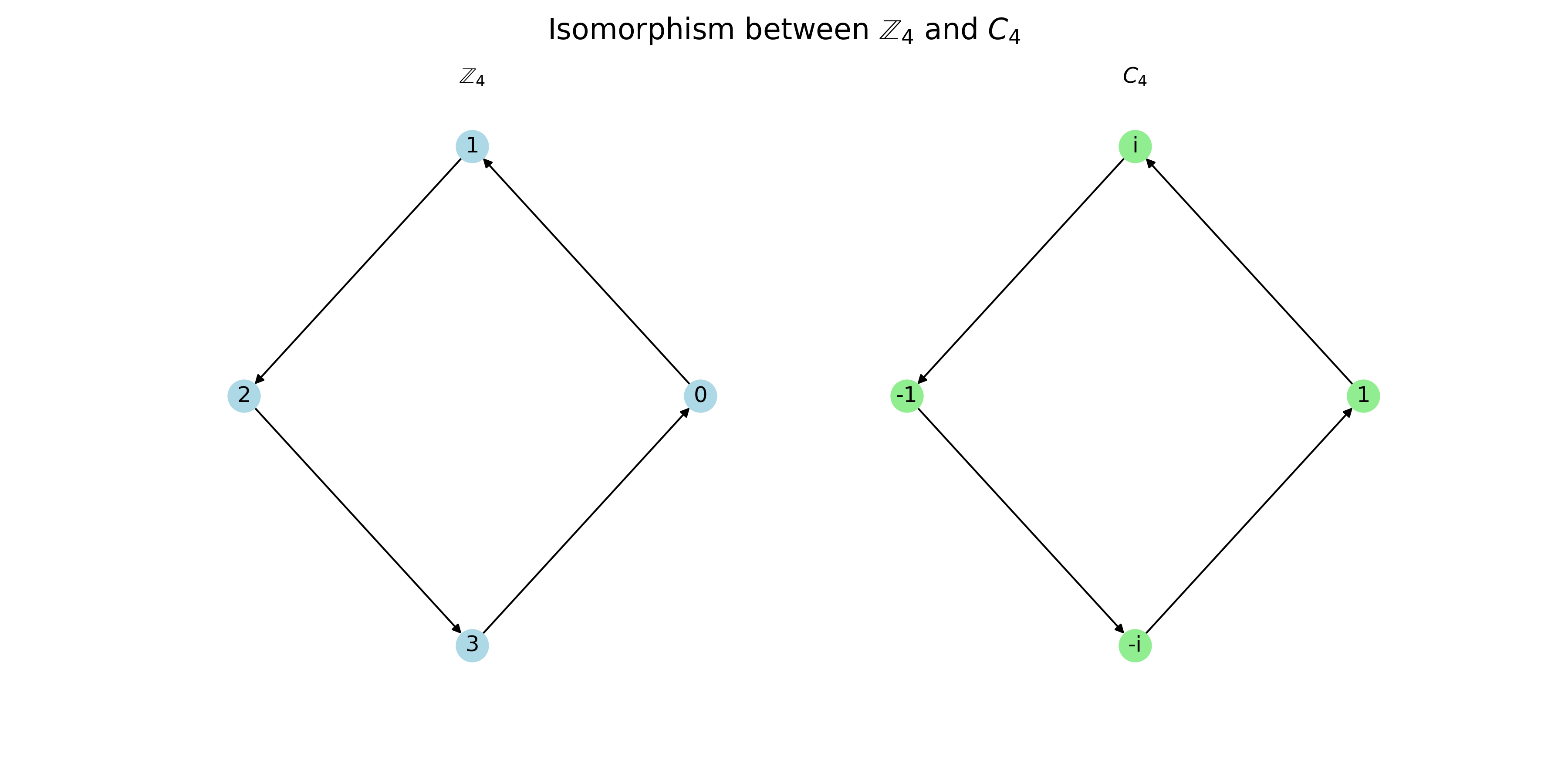
有没有发现，他俩不但可以一一对应，连各自内部的运算的作用也一样。

• 整数加法群 $\mathbb{Z}_4$：由元素 {0, 1, 2, 3} 组成，运算是模 4 加法。

• 四元旋转群 $C_4$：由旋转角度 {0°, 90°, 180°, 270°} 组成，运算是旋转的叠加。

每运算一次的效果都是指向下一个元素。直觉上就能感觉到他们的同构性。

可以构建映射关系：

• 映射关系：将 $\mathbb{Z}_4$ 中的元素映射到 $C_4$ 中对应的旋转角度。

• 运算一致性：在 $\mathbb{Z}_4$ 中的加法对应于 $C_4$ 中的旋转叠加。例如，$1 + 2 = 3$ 对应于 $90° + 180° = 270°$。

还不满足？我们继续验证！

好的，我们来验证子群之间的同构关系。

$\mathbb{Z}_4$ 的子群：

• $\{0\}$

• $\{0, 2\}$（因为 $2 + 2 \equiv 0 \pmod{4}$）

$C_4$ 的子群：

• $\{e\}$

• $\{e, r^2\}$（因为 $(r^2)^2 = e$）

他俩也完全同构！

通过映射 $\phi: \mathbb{Z}_4 \to C_4$：

• $\phi(\{0\}) = \{e\}$

• $\phi(\{0, 2\}) = \{e, r^2\}$

我们来看看陪集？

$\mathbb{Z}_4$ 的子群 $\{0, 2\}$ 左陪集：

• $\{0, 2\} + 0 = \{0, 2\}$

• $\{0, 2\} + 1 = \{1, 3\}$

• $\{0, 2\} + 2 = \{2, 0\}$

• $\{0, 2\} + 3 = \{3, 1\}$

$C_4$ 的子群 $\{e, r^2\}$ 左陪集：

• $\{e, r^2\} \cdot e = \{e, r^2\}$

• $\{e, r^2\} \cdot r = \{r, r^3\}$

• $\{e, r^2\} \cdot r^2 = \{r^2, e\}$

• $\{e, r^2\} \cdot r^3 = \{r^3, r\}$

还是同构的！$\phi: \mathbb{Z}_4 \to C_4$：

• $\phi(\{0, 2\}) = \{e, r^2\}$

• $\phi(\{1, 3\}) = \{r, r^3\}$