八数码问题(A-star 解)
八数码
其实就是拼图。九宫格,放七数,余一空可与纵横邻数交换。求最短移动路径,使九宫格从起始状态变换到目标状态。
A-star
A-star 算法的核心是引入代价,有限选择代价低的边界点进行访问。代价等于历史代价+未来代价。
边界(frontier)
边界:访问过的点,与未访问过的点的交界上,那些正在估算代价的点。
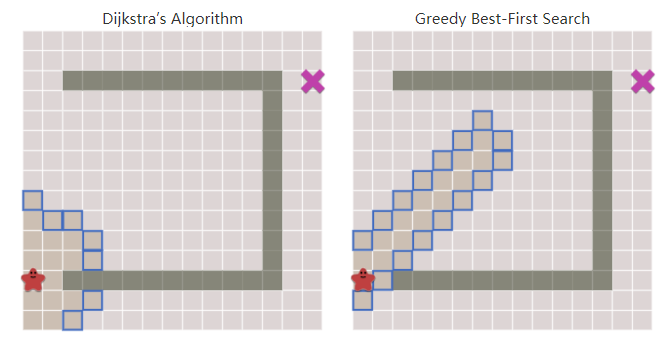
上图中,蓝色的区域就是边界。初始条件下,起点的邻接点就是边界点。对于每个点,可以计算其代价。A*算法的核心思想,就是选取代价最少的边界点优先访问。
代价
A * 的代价计算公式:
整体代价历史代价未来估计代价(1)整体代价=历史代价+未来估计代价
即:假设我们要从 S 点到 T 点的最短路径,则当途径点 N 时,计算 S-N-T 的代价为 S-N 的实际代价加上 N-T 的估计代价。
- 当估计代价变为
0时,A* 退化为 Dijkstra 算法
当边界点与目标重合时,寻路完成。
那么,完成之后我们如何确定路径时怎样的呢?类似 Dijkstra,我们维护一个 Prev 数组,记录了每个节点的上一步节点。你可以将其视作一个向量场:
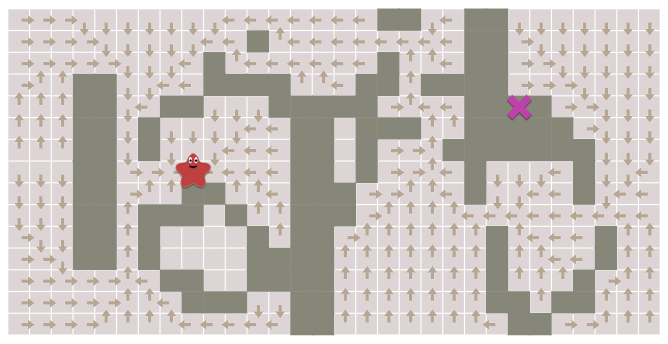
这样我们可以不断回溯,直到起点。
八数码问题的 A-star 解

代码说明
代码整体结构
为了便于展示,我使用了 HTML 语言编写。整体结构如下:
1<!DOCTYPE html>
2<html lang="en">
3
4<head>
5 <meta charset="UTF-8">
6 <meta http-equiv="X-UA-Compatible" content="IE=edge">
7 <title>8-puzzle</title>
8</head>
9
10<body>
11 #样式表#
12 <div id="app">
13 <pre id="stdout"></pre>
14 <div id="ans"></div>
15 </div>
16 <script>
17 #工具函数#
18 write("Welcome to the 8-puzzle game!");
19 let goalState = [
20 [0, 1, 2],
21 [3, 4, 5],
22 [6, 7, 8]
23 ];
24 do {
25 initState = generateState();
26 }
27 while (!isResolvable(initState, goalState));
28 writeln("<p>Initial state:</p>");
29 displayState(initState);
30 writeln("<p>Goal state:</p>");
31 displayState(goalState);
32 writeln("<p>Start searching...</p>");
33 #寻路算法#
34 let path = aStar(initState, goalState);
35 for (let i = 0; i < path.length; i++) {
36 let state = unhashState(path[i]);
37 displayState(state, "ans", (str) => {
38 return `<div class="state">${str}</div>`
39 });
40 }
41 </script>
42</body>
43
44</html>
样式表
这部分是为了进行梯度着色和排版,无关紧要。
1 <style>
2 .num-0 {
3 background-color: #ffffff;
4 }
5
6 .num-1 {
7 background-color: #bcffde;
8 }
9
10 .num-2 {
11 background-color: #52ffac;
12 }
13
14 .num-3 {
15 background-color: #00ff84;
16 }
17
18 .num-4 {
19 background-color: #00ce6a;
20 }
21
22 .num-5 {
23 background-color: #00a153;
24 }
25
26 .num-6 {
27 background-color: #008344;
28 }
29
30 .num-7 {
31 background-color: #006434;
32 }
33
34 .num-8 {
35 background-color: #00381d;
36 }
37
38 .num {
39 display: inline-block;
40 width: 32px;
41 height: 32px;
42 }
43
44 #stdout {
45 box-sizing: border-box;
46 }
47
48 #app {
49 margin: 1em;
50 box-sizing: border-box;
51 }
52
53 #ans {
54 display: flex;
55 flex-flow: wrap;
56 }
57
58 /* clear broswer style*/
59 html,
60 body,
61 html {
62 margin: 0;
63 padding: 0;
64 }
65 .state {
66 display: block;
67 width: 120px;
68 height: 120px;
69 }
70 pre {
71 font-family: monospace;
72 }
73 </style>
工具函数
输入输出
这里利用网页进行输出的模拟。
write(params, target = "stdout"): 向标准输出输出字符串-
params: 字符串 -
target: 可选参数,默认为stdout,表示输出到标准输出,可以是stdout或ans
-
1 function write(params, target = "stdout") {
2 document.getElementById(target).innerHTML += `${params}`;
3 }
writeln(params, target = "stdout"): 向标准输出输出字符串,并在末尾添加换行符-
params: 字符串 -
target: 可选参数,默认为stdout,表示输出到标准输出,可以是stdout或ans
-
1 function writeln(params, target = "stdout") {
2 document.getElementById(target).innerHTML += `${params}\n`;
3 }
function read(hint, postproc): 读取用户输入,并返回输入的字符串
1 function read(hint, postproc) {
2 var input = prompt(hint);
3 if (input == null) {
4 return null;
5 }
6 if (postproc != null) {
7 input = postproc(input);
8 }
9 return input;
10 }
generateState = ()随机初始化拼图状态return: 初始状态
1 let generateState = () => {
2 let state = [];
3 let left = [1, 2, 3, 4, 5, 6, 7, 8, 0];
4 for (let i = 0; i < 3; i++) {
5 state[i] = [];
6 for (let j = 0; j < 3; j++) {
7 let randIndex = Math.floor(Math.random() * left.length);
8 state[i][j] = left[randIndex];
9 left.splice(randIndex, 1);
10 }
11 }
12 return state;
13 }
displayState(state, target = "stdout", postproc = null): 显示拼图状态-
state: 拼图状态 -
target: 可选参数,默认为stdout,表示输出到标准输出,可以是stdout或ans -
postproc: 可选参数,默认为 null,表示不进行任何处理,可以是函数
-
1 function displayState(state, target = "stdout", postproc = null) {
2 var str = "";
3 // 3x3 board
4 for (var i = 0; i < 3; i++) {
5 for (var j = 0; j < 3; j++) {
6 s = state[i][j]
7 str += `<span class="num num-${s}">${s}</span>`;
8 }
9 str += "\n";
10 }
11
12 if (postproc != null) {
13 str = postproc(str);
14 }
15 write(str, target);
16 }
numberOfInversions(seq): 计算序列中的逆序数-
seq: 序列 -
return: 逆序数
-
1 function numberOfInversions(seq) {
2 let count = 0;
3 for (let i = 0; i < seq.length; i++) {
4 for (let j = i + 1; j < seq.length; j++) {
5 if (seq[i] > seq[j]) {
6 count++;
7 }
8 }
9 }
10 return count;
11 }
flatten(state): 将拼图状态转换为一维数组-
state: 拼图状态 -
return: 一维数组
-
1 function flatten(arr) {
2 return arr.reduce((a, b) => a.concat(b), []);
3 }
isSolvable(state): 判断拼图是否可解-
state: 拼图状态 -
goalState: 拼图目标状态 -
return: 可解性
-
1 function isResolvable(state, goalState) {
2 let seq = flatten(state);
3 let goalSeq = flatten(goalState);
4 return numberOfInversions(seq) % 2 == numberOfInversions(goalSeq) % 2;
5 }
calcNum2loc(state): 计算拼图状态中每个数字的位置-
state: 拼图状态 -
return: 数字位置映射
-
1
2 function calcNum2loc(state) {
3 // 计算每个数字的位置,相当于一个反向索引
4 let num2loc = {};
5 for (let i = 0; i < 3; i++) {
6 for (let j = 0; j < 3; j++) {
7 num2loc[state[i][j]] = [i, j];
8 }
9 }
10 return num2loc;
11 }
cost(state, goalState): 计算拼图距离目标状态的代价(这里采用曼哈顿距离)-
state: 拼图状态 -
goalState: 拼图目标状态 -
return: 代价
-
1 // 采用曼哈顿距离,即当前各棋子均移动到目标位置的总移动距离
2 function cost(state, goalState) {
3 let goalNum2loc = calcNum2loc(goalState);
4 let cost = 0;
5 for (let x = 0; x < 3; x++) {
6 for (let y = 0; y < 3; y++) {
7 let num = state[x][y];
8 if (num == 0) {
9 continue;
10 }
11 let goalX = goalNum2loc[num][0];
12 let goalY = goalNum2loc[num][1];
13 cost += Math.abs(x - goalX) + Math.abs(y - goalY);
14 }
15 }
16 return cost;
17 }
state2hash(state): 计算拼图状态的哈希值-
state: 拼图状态 -
return: 哈希值
-
1
2 let state2hash = (state) => {
3 let flat = flatten(state);
4 let hashval = 0;
5 for (let i = 0; i < flat.length; i++) {
6 hashval = hashval * 10 + flat[i];
7 }
8 return hashval;
9 }
unhashState(hashval): 将哈希值转换为拼图状态-
hashval: 哈希值 -
return: 拼图状态
-
1 let unhashState = (hashval) => {
2 let state = [
3 [0, 0, 0],
4 [0, 0, 0],
5 [0, 0, 0]
6 ];
7 for (let i = 0; i < 3; i++) {
8 for (let j = 0; j < 3; j++) {
9 state[2 - i][2 - j] = hashval % 10;
10 hashval = Math.floor(hashval / 10);
11 }
12 }
13 return state;
14 }
minFxStateHash(open, fx): 计算拼图状态的最小fx值对应的哈希值-
open: 开放列表,即“待访问”列表 -
fx: fx值映射
-
1
2 // 寻找 open 中代价最小的状态
3 function minFxStateHash(open, fx) {
4 let minFxHash = open[0];
5 for (let i = 1; i < fx.length; i++) {
6 if (fx[i] < minFxHash) {
7 minFxHash = fx[i];
8 }
9 }
10 return minFxHash;
11 }
swap(newState, zeroLoc, newLoc): 交换拼图状态中的两个数字-
newState: 拼图状态 -
zeroLoc: 数字0的位置 -
newLoc: 数字0的新位置
-
1 function swap(newState, zeroLoc, newLoc) {
2 let temp = newState[zeroLoc[0]][zeroLoc[1]];
3 newState[zeroLoc[0]][zeroLoc[1]] = newState[newLoc[0]][newLoc[1]];
4 newState[newLoc[0]][newLoc[1]] = temp;
5 }
关键算法
1 function aStar(initState, goalState) {
2 // 初始化. fx = gx + hx
3 let openStates = [], // 待访问列表,存储一系列 open 状态。相当于边界列表
4 openState2fx = {}, // fx 用于存储每个 open 状态的总代价
5 openState2gx = {}, // gx 用于存储每个 open 状态的现代价
6 // 我们这里不用 hx,因为 hx 可以通过代价函数计算
7 closed = {}, // 关闭列表,存储一系列 closed 状态。相当于障碍列表,表示已经访问过的状态
8 parent = {}; // 父节点,用于路径回溯
9 // 可能的移动方向。主语是空格
10 let moves = [
11 [1, 0], // 向右移动
12 [-1, 0], // 向左移动
13 [0, 1], // 向下移动
14 [0, -1] // 向上移动
15 ];
16 // 初始化 open 列表。将起点状态加入 open 列表,并计算其 gx ,fx 值
17 let curHash = state2hash(initState);
18 let goalHash = state2hash(goalState);
19 let curState = initState;
20 openStates.push(curHash);
21 openState2gx[curHash] = 0;
22 openState2fx[curHash] = cost(curState, goalState);
23
24 // 开始搜索
25 while (openStates.length > 0) {
26 // 寻找 open 列表中代价最小的状态,将其加入 closed 列表并从 open 列表中移除,设为当前状态
27 curHash = minFxStateHash(openStates, openState2fx);
28 curState = unhashState(curHash);
29 openStates.splice(openStates.indexOf(curHash), 1);
30 closed[curHash] = true;
31 // 如果当前状态是目标状态,则结束搜索
32 if (curHash == goalHash) {
33 alert("success!");
34 break;
35 }
36 // 对当前状态的每一个可能的移动方向进行搜索
37 let curNum2loc = calcNum2loc(curState);
38 let zeroLoc = curNum2loc[0];
39 let success = false
40 for (let i = 0; i < moves.length; i++) {
41 let newLoc = [zeroLoc[0] + moves[i][0], zeroLoc[1] + moves[i][1]];
42 // 如果移动后的位置不合法,则跳过
43 if (newLoc[0] < 0 || newLoc[0] > 2 || newLoc[1] < 0 || newLoc[1] > 2) {
44 continue;
45 }
46 // 计算新状态。即通过向 moves[i] 方向移动数字0
47 let newState = curState.map(row => [...row]);
48 swap(newState, zeroLoc, newLoc);
49 // 计算新状态的 gx, fx 值
50 let newHash = state2hash(newState);
51 let newGx = openState2gx[curHash] + 1;
52 let newFx = newGx + cost(newState, goalState);
53 openState2fx[newHash] = newFx;
54 openState2gx[newHash] = newGx;
55 if (newHash == goalHash) {
56 alert("success!");
57 success = true
58 break;
59 }
60 // 如果新状态不在 open 列表中,则加入 open 列表
61 if (!(newHash in closed)) {
62 openStates.push(newHash);
63 // 记录新状态的父节点,完善回溯向量场
64 parent[newHash] = curHash;
65 }
66 }
67 if (success) {
68 break;
69 }
70 }
71 // 回溯路径
72 let path = [];
73 let initHash = state2hash(initState);
74 while (curHash != initHash) {
75 path.push(curHash);
76 curHash = parent[curHash];
77 }
78 // 逆序
79 path.reverse();
80 path.push(goalHash)
81 return path;
82 }
83
84 let path = aStar(initState, goalState);
85 for (let i = 0; i < path.length; i++) {
86 let state = unhashState(path[i]);
87 displayState(state, "ans", (str) => {
88 return `<div class="state">${str}</div>`
89 });
90 }
