如何重新发明一个 B-tree ？

本文目标

文本旨在搞懂下列问题：

• 什么是 B 树？

  • B 树存放的是什么数据？

  • B 树怎么存放数据？

  • B 树有何优势？

  • 如何对 B 树进行 CRUD？

• 如何用代码实现 B 树？

什么是 B 树？

我发现很多教程上来就给一大段定义，结果看完也不知道 B 树是干嘛的。接下来，我们自己重新发明一个 B 树！

其实，B 树的核心功能是查找。输入：Key（关键字），输出：Node（该关键字对应的结点）。

• Key 可以是任何类型，比如整数、小数、字符、字符串。只要满足偏序性，即可以比较大小。

• 与 Key 一起存放在树结点里的主要是 子结点 的指针。

• 另外，可能还顺带存放一些元数据。

B 树的诞生是为了避免 BST 层级过多 的问题。那么我们就扁平化管理，每个 Node 多存一点数据.

自然从而可以构想出下面的结构：

┌────────────┬────────┬───────────┐
│ meta data  │  keys  │  children │
└────────────┴────────┴───────────┘

但实际上，我们不可能就存个 Key 吧？比如做个哈希表，总要取值出来。所以可以增加 values 域：

┌────────────┬────────┬───────────┬────────────┐
│ meta data  │  keys  │  children │   values   │
└────────────┴────────┴───────────┴────────────┘

并且确保 values 的元素个数与 keys 的个数相同，从而一一对应。

---

设计合适的插入算法

那么如何为其构造子结点呢？B 树的特点是一个结点有多个 key。我们让这些 key 升序排列（假定 keys = [1, 4, 9, 16]）：

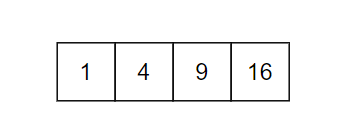
此时，插入一值，比如 8. 一个自然的想法就是放到 4 和 9 之间。

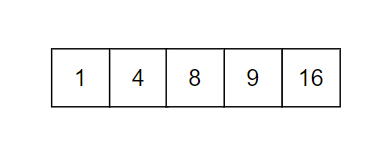
这样没问题。但是总不能一直这样插入，不然就变成线性表了。我们假定最大 5 个，再多就满了。那么此时再插入一个 5，一个自然的想法是：

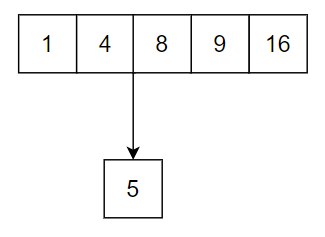
我们创建了一个子结点！

同理，可以创建很多子结点。如果每个 Node 的 key 最多 5 个，则最多可以创建 6 个子结点：

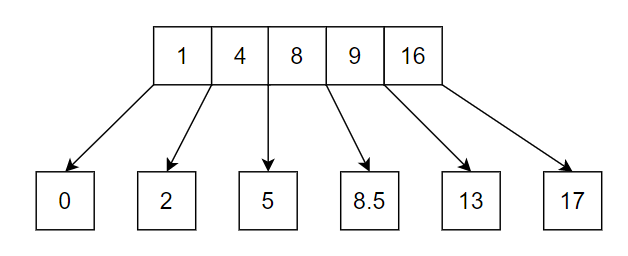
实际上，每个子结点的容量最大都是 5 个。那么还能继续存。比如往 0 结点上继续插入 -4,-3,-1,0：

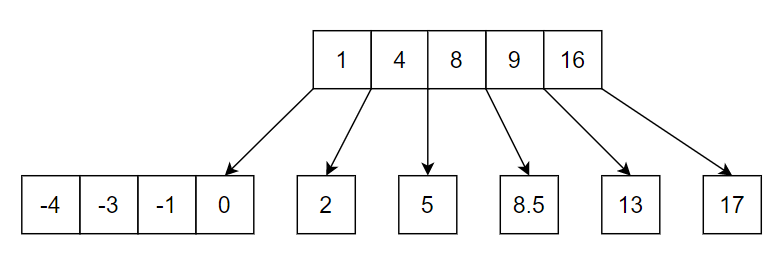
这是一种朴素的 B 树思想。

最简单的想法：有序插入

这样会不会存在问题呢？不妨找一个极端的例子，插入 $1,\cdots,20$

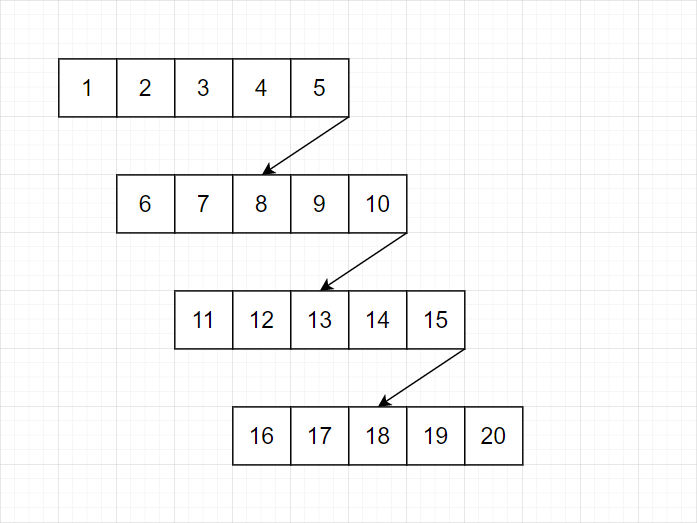
我们发现：若是采用简单按大小顺序插入的策略，树很容易失衡。

为了避免失衡，必须引入平衡算法。

叶子尽早平衡（Preemptive B-Tree）的插入策略

那么能否采用尽早平衡的策略？也就是说，能拆分就拆分。

• 一个叶子结点达到三个，就将中间的提出到上一层结点

• 中间层的结点一旦满了（本例为 5 个满），就继续向上提出。

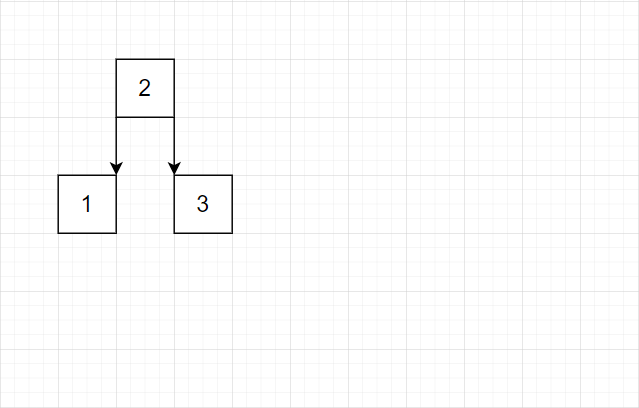
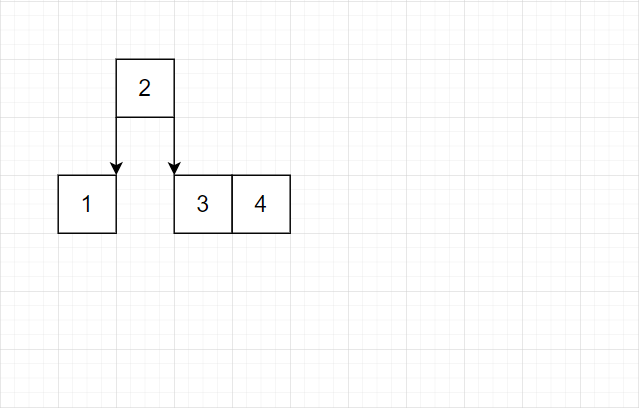
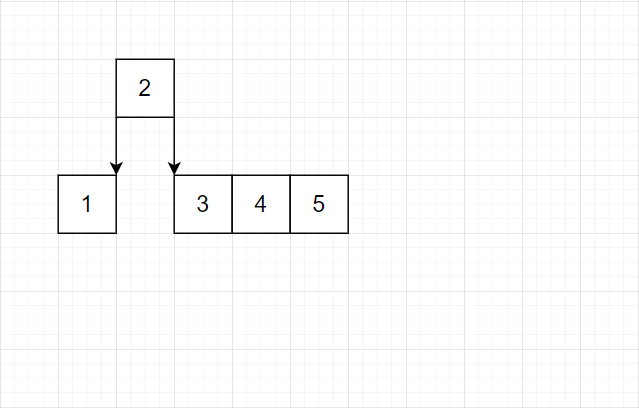
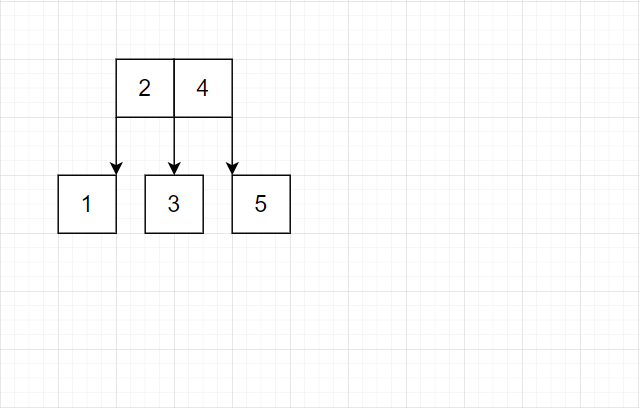
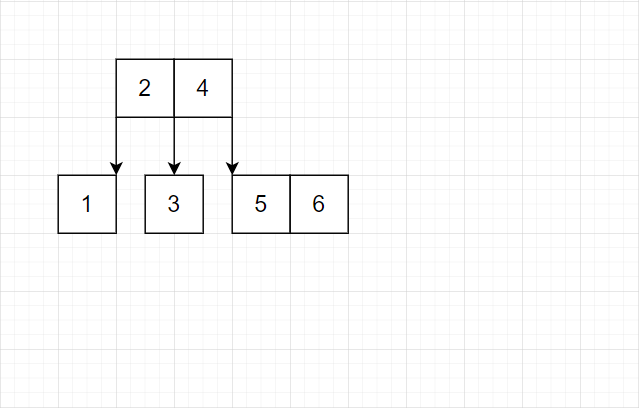
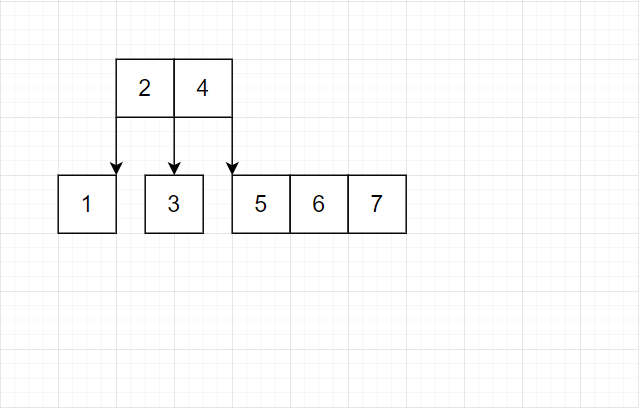
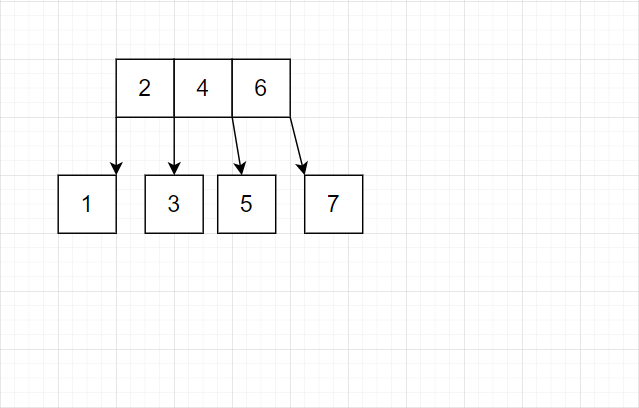
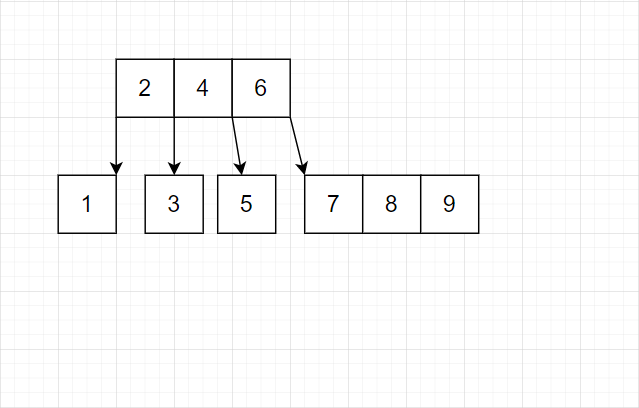
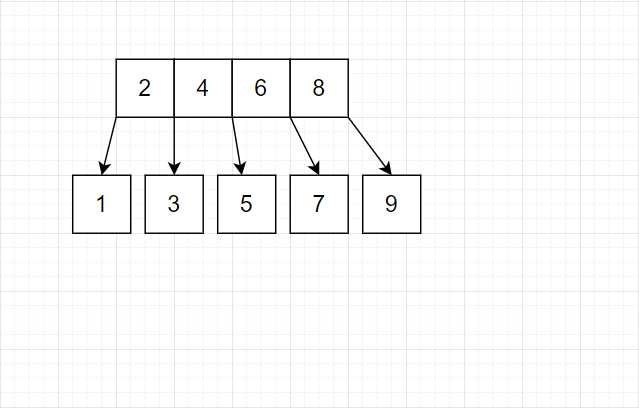
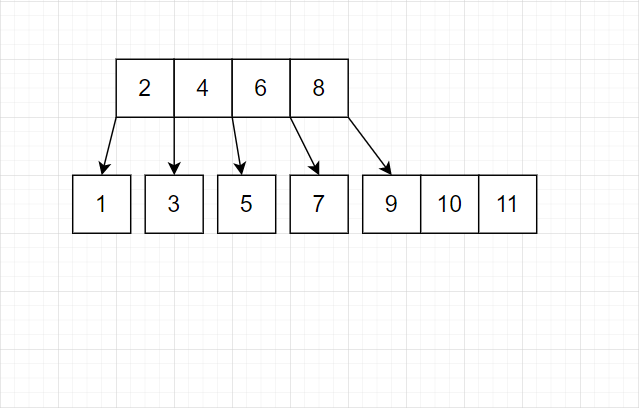
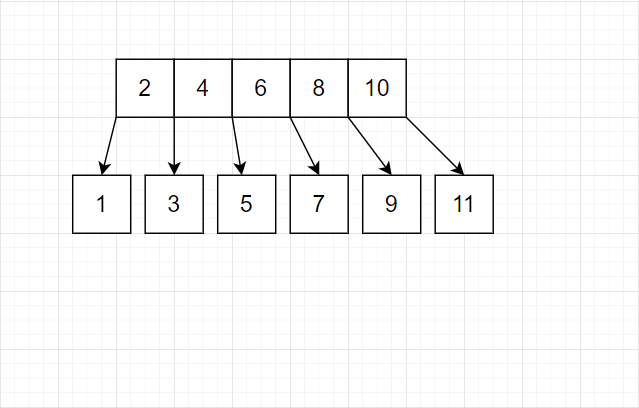
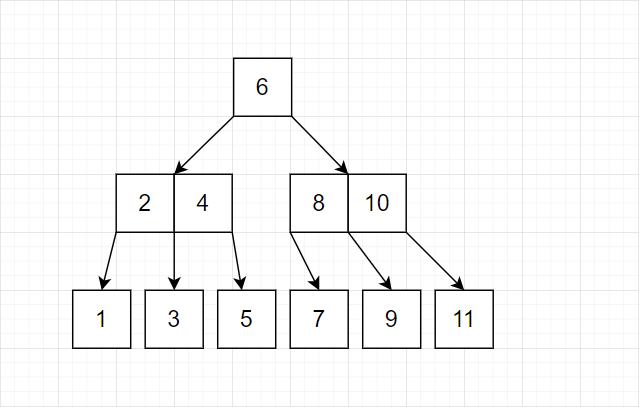
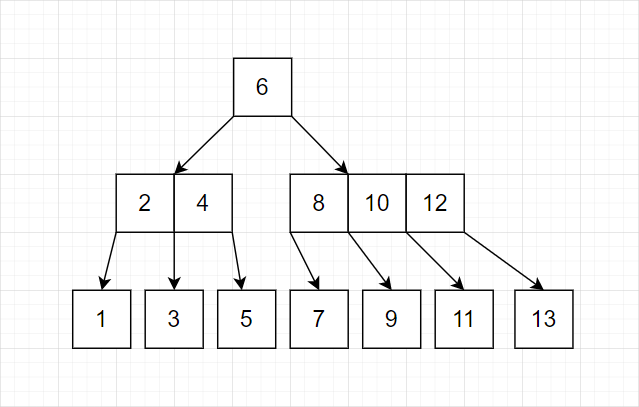
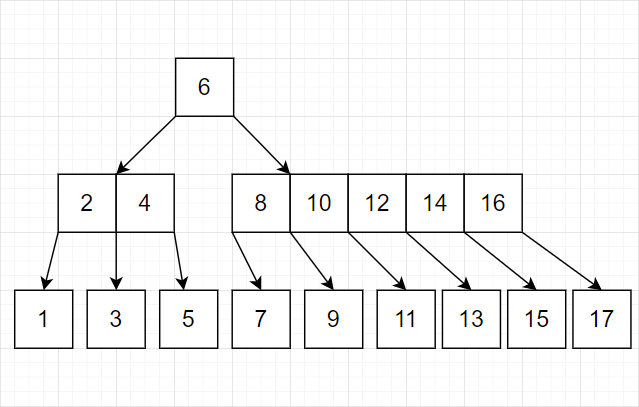
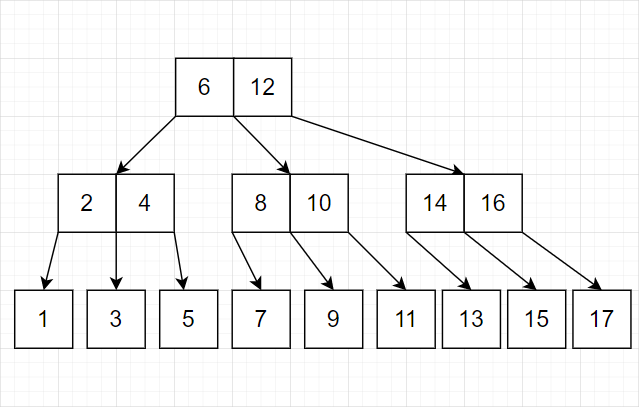
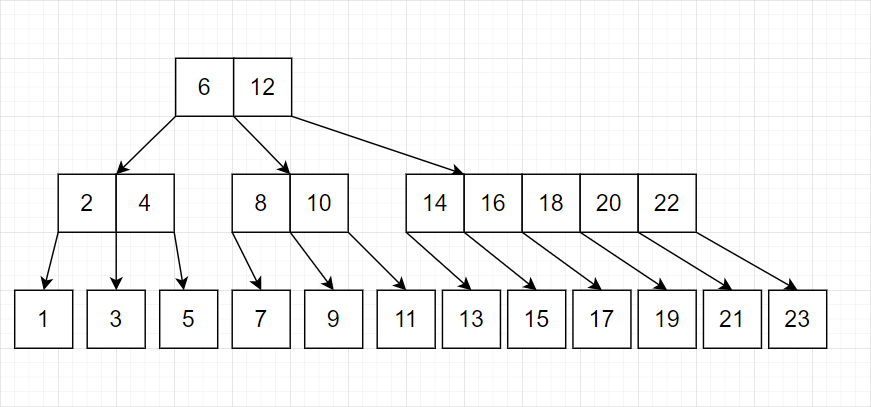
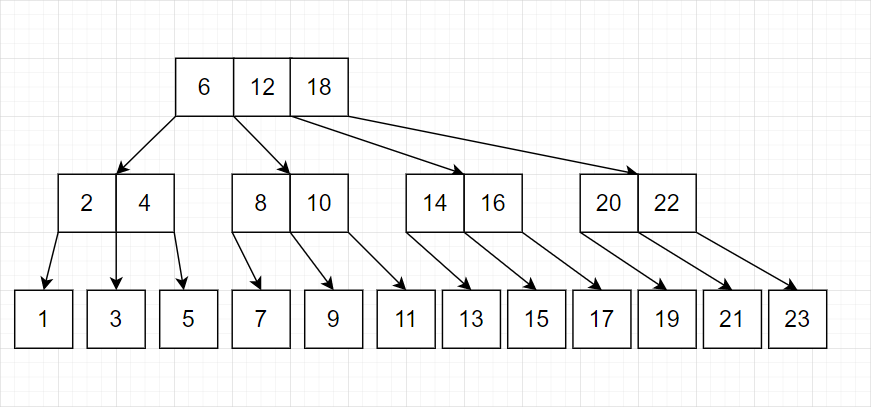
我们发现这种策略完全可行。有这样的特点：最底层几乎总是单个结点。

拖延平衡（Regular B-Tree）的插入策略

既然上面的策略，对于中间结点是满了才提出到上层，为啥不对所有结点一视同仁呢？

我们不妨试试：

• 对于任意结点，只在结点满时平衡。

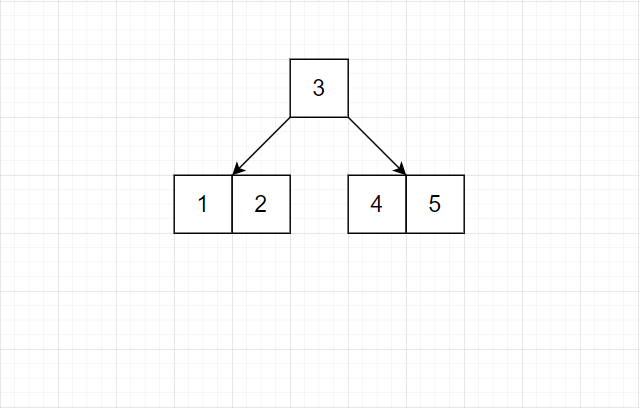
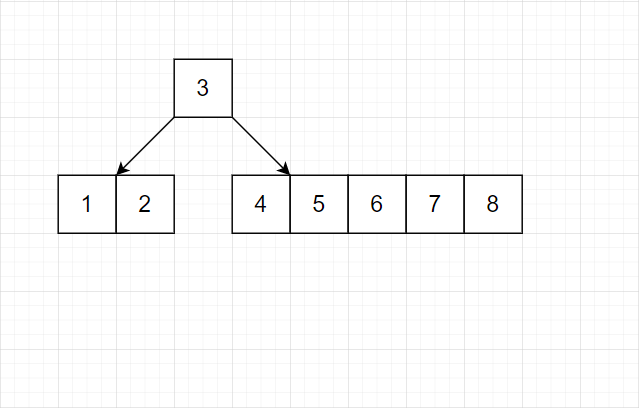
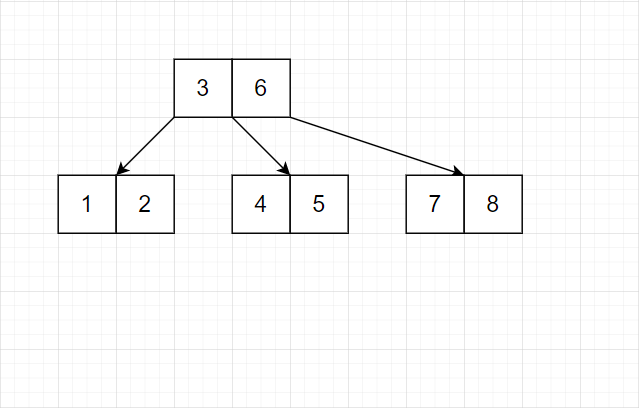
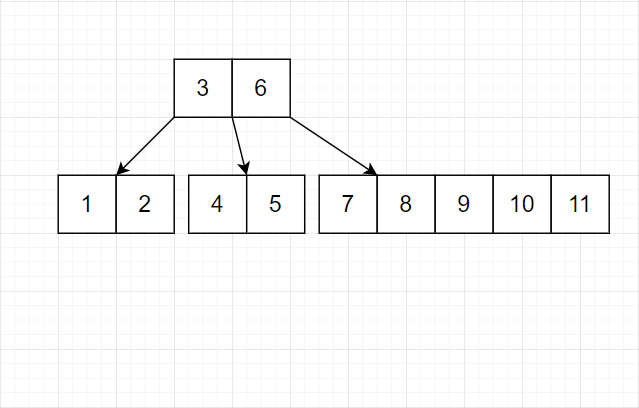
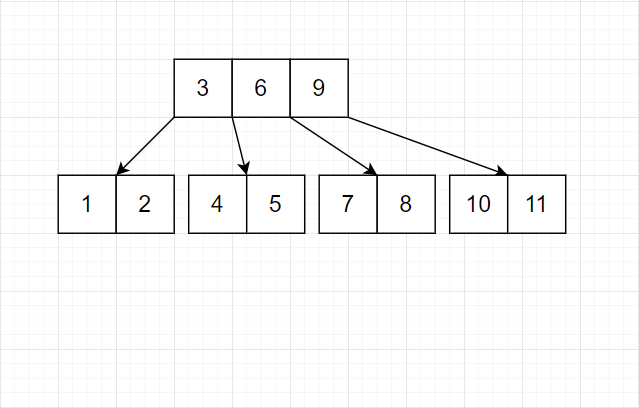
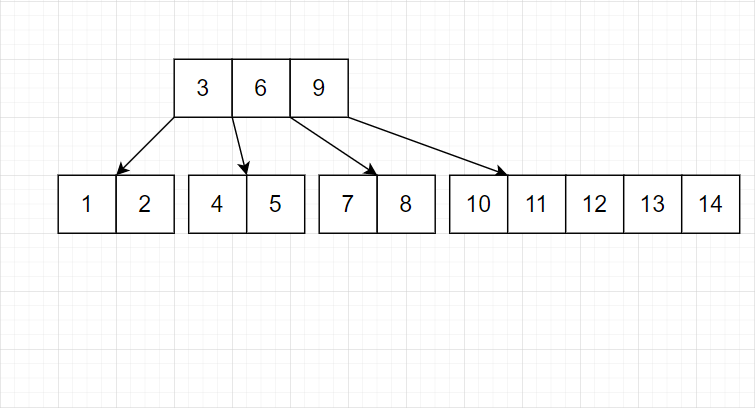
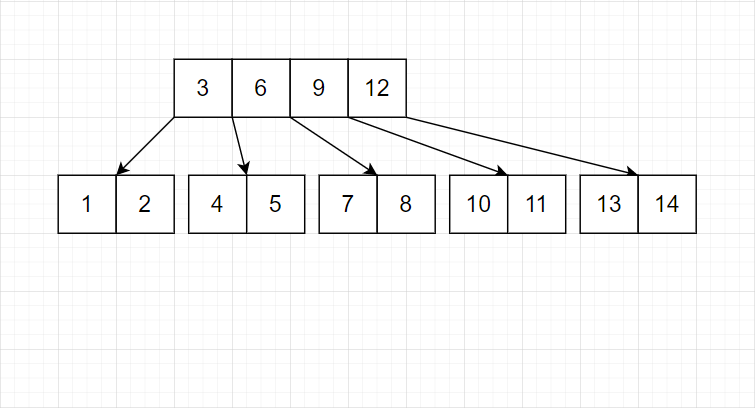
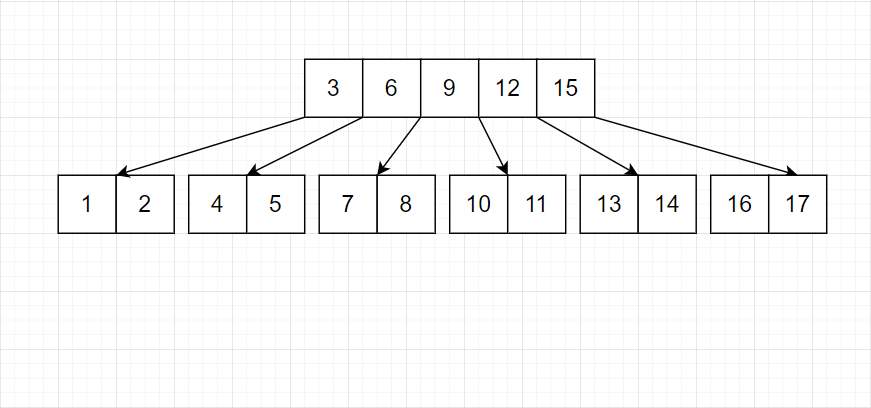
注意，上层也满了，所以也得调整。

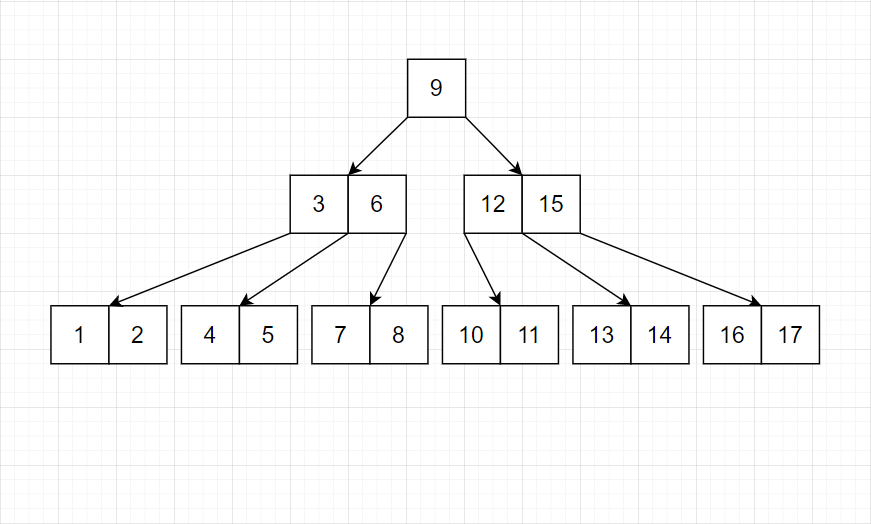
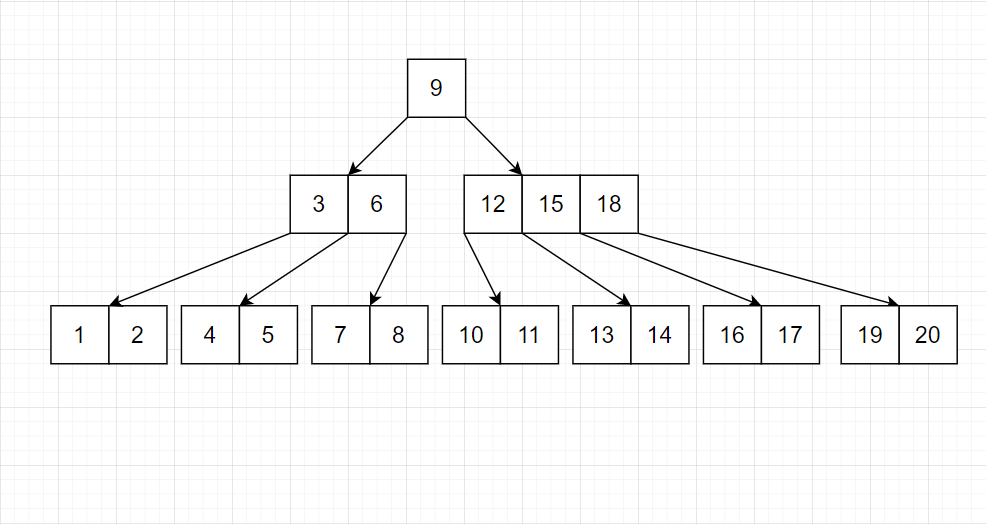
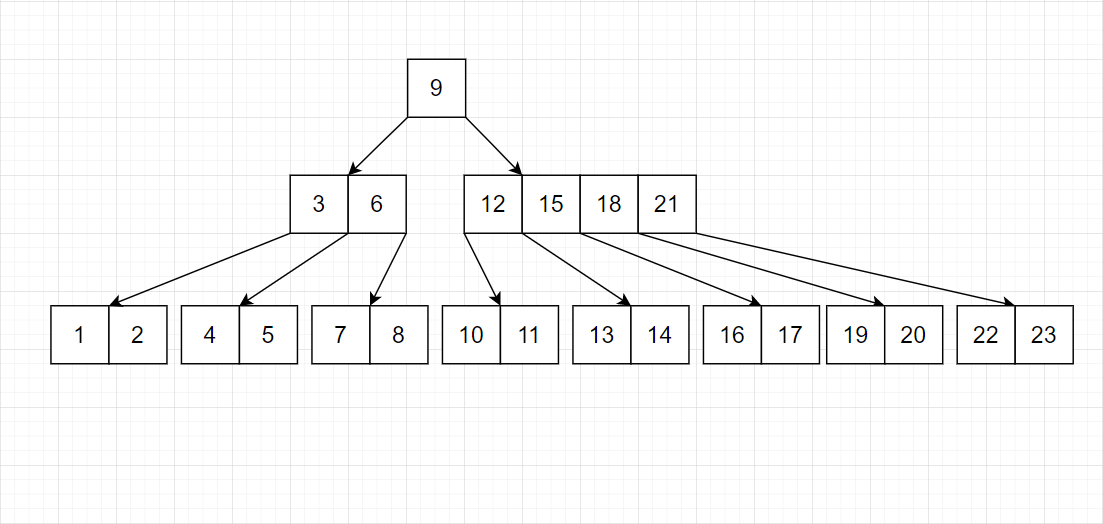
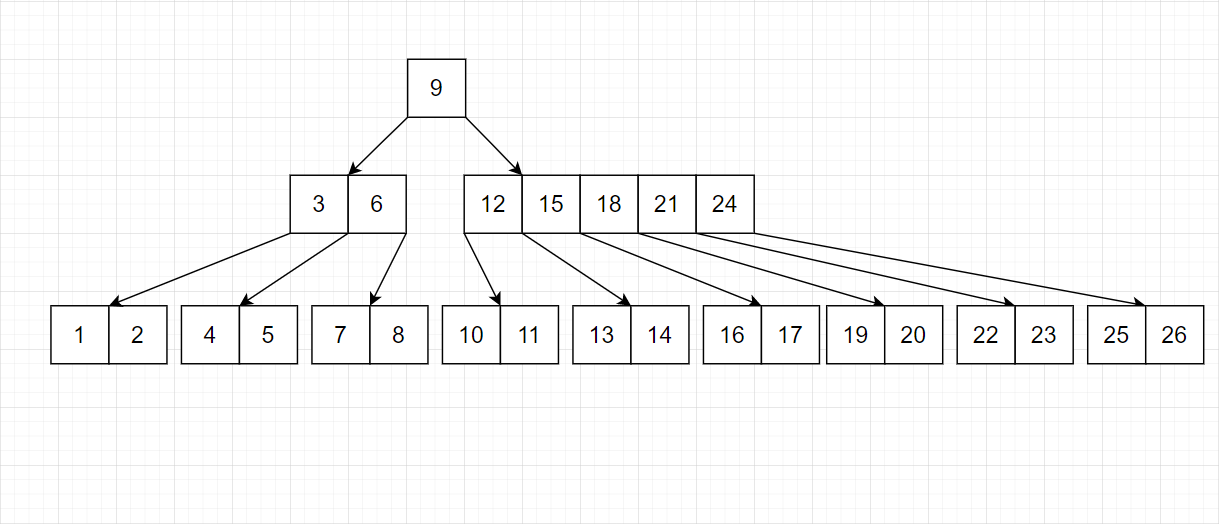
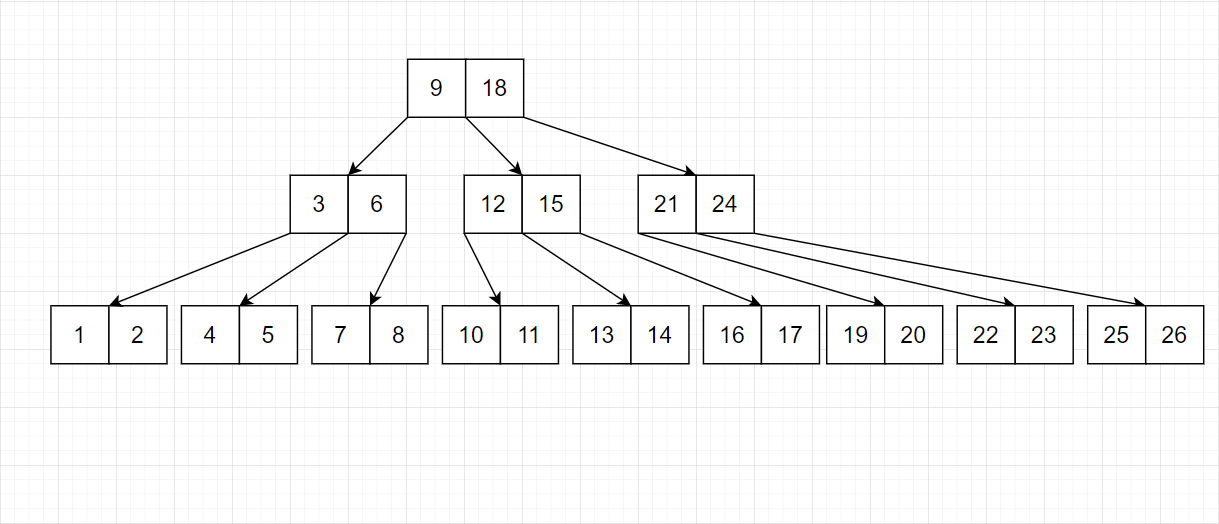
我们发现，树的平衡性非常好。并且结点均是完美的等差数列。并且底层的连续性也不错。

这就是常规 B-树采用的策略。

删除策略

如果要从下面的 B-Tree 删除 11，如何操作呢？

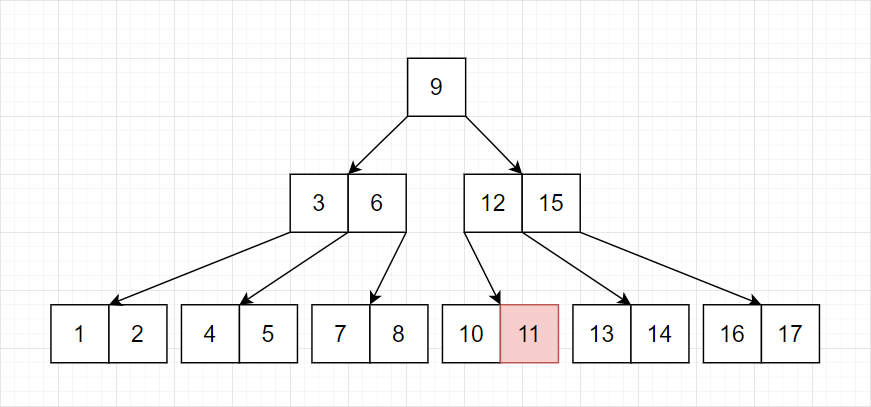
第一步，找到并拿掉它。查找策略很简单，二分即可。

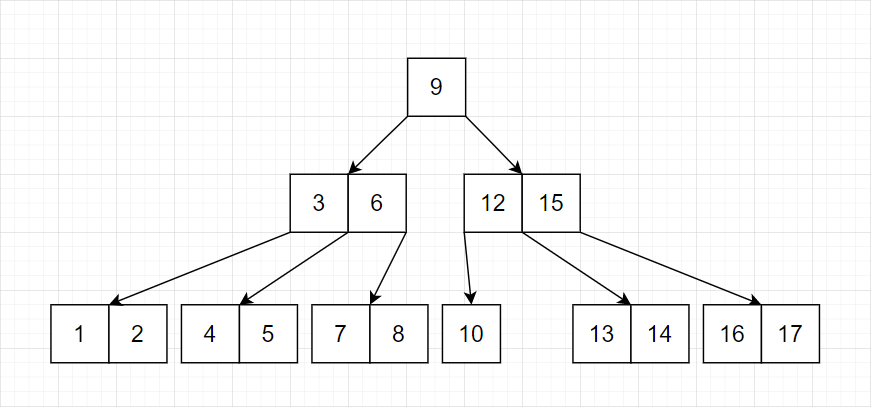
第二步，由于空缺出一个位置，所以从上面一层寻找替补，并清除多余的连接。

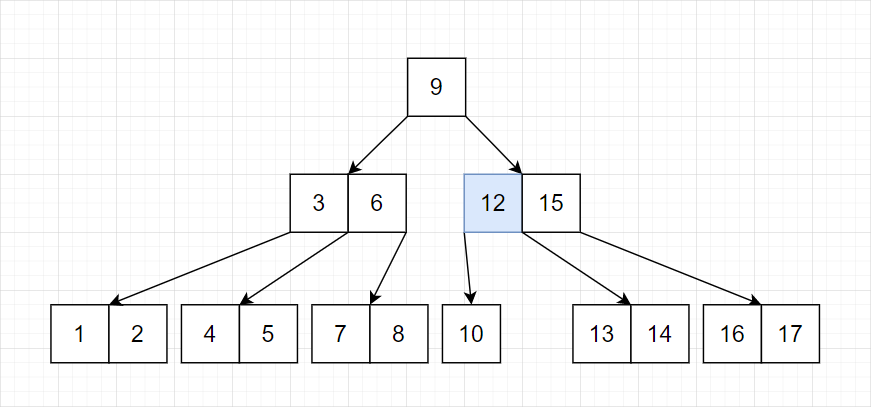
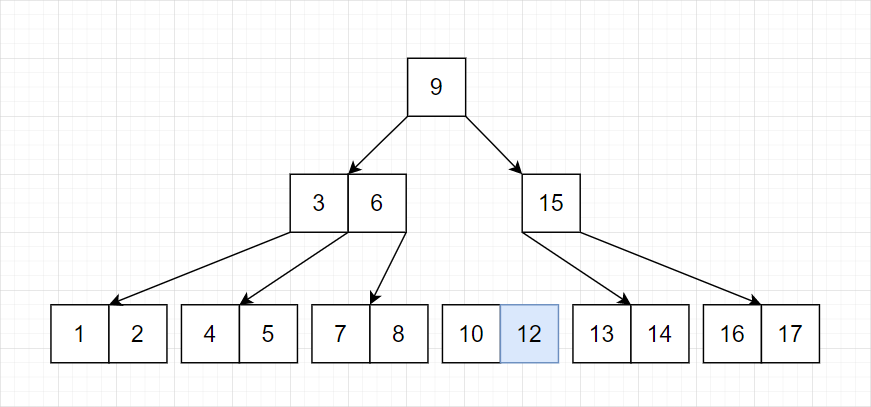
调整连接

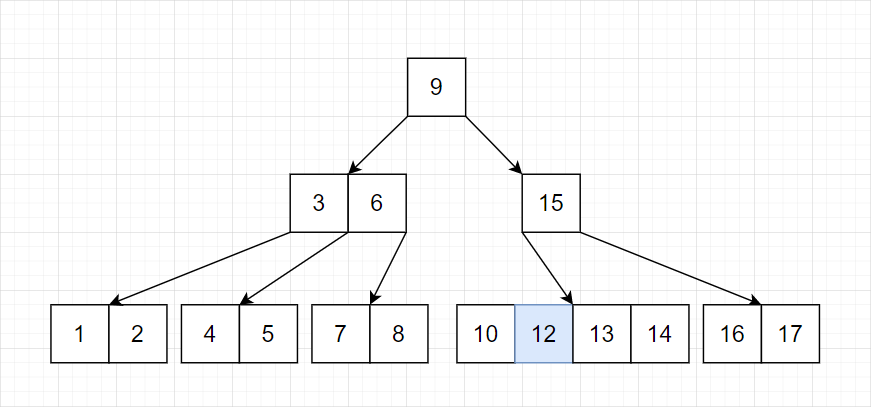
由于此时 9 已经不满足独立出去的条件（下层未满），所以需要向下合并：

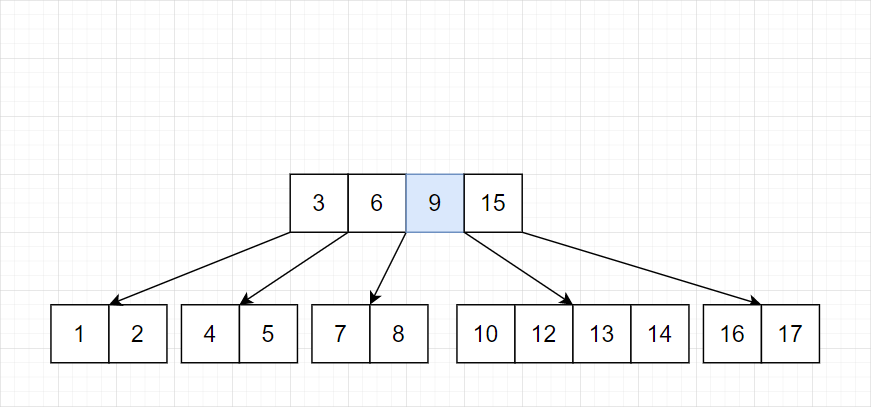
删除操作就完成了。

删除后需要旋转调整的情况

考虑下面的 Max=3 的 B-Tree 中删除 11

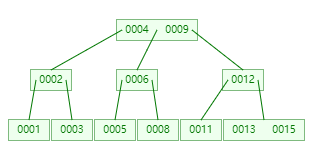
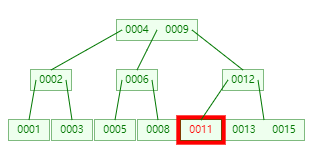
为了保持平衡，需要将右边的兄弟 13 移向左上方的 12，而 12 移向左下方占据原来 11 的位置：

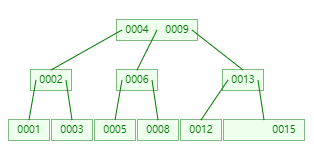
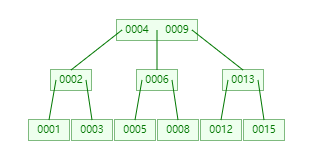
删除总结：

• 如果删除后能维持 B 树，则不用调整。

• 否则需要上层向下合并。重复直到满足 B 树。

  • 如果向下合并导致上层位置空出，则需要通过左旋/右旋从后代中选出新的占据位置。

B 树的实现

实现的话可以用各种语言，为了便于理解思路，我这里采用 Javascript.